分数で遊んで算数のセンスを揺さぶっておこう! 次の問題を考えてください。 中高生の諸君も小学生の問題だからといって無視せずにトライしてみてください。 中学生・高校生になって数学がだんだんと分からなくなるのも、こういった整 […]
adminさんの記事一覧(2 / 7ページ目)
整数を素因数分解する力と輪環の順 | 数と友達になって考え切る(3)
3つの整数で遊んで算数のセンスを揺さぶっておこう! 次の問題を考えてください。 中高生の諸君も小学生の問題だからといって無視せずにトライしてみてください。 中学生・高校生になって数学がだんだんと分からなくなるのも、こうい […]
「3×3×3は3を3回かける」なんて説明で「3を0回かけて1」が説明できるの?
よく、2×2×2×2×2と書いて「2を5回かける」とか、3×3×3と書いて「3を3回かける」なんて書いてありますよね。 さて、間違っているというわけじゃないんですよ。 みんな、そういう風に言ってますものね。 でも、なんか […]
小学生のための4色問題等至極の5題 | なんと!場合の数がヨ・タ・ヨ・タ歩けば分かる!
塾へ行くのが嫌で通塾していなかったのに、いつも成績はクラスでトップの子を指導した際の残存資料より、下記の『場合の数』5題を通して、そのポイントやコツを掴んでいただければと思います。 そんな彼も、結局は、FAX方式にプラス […]
AI(人工知能)学習は本当に生徒の学力を伸ばせるのか?
AI(人工知能)のお祭り騒ぎ 昨今、車で街中を走っていますと、学習塾に「AI学習」などと書かれた看板をよく目にするようになりました。 今や、学習塾に限らず、あらゆる業種において「AI」「AI」と連呼されて耳たこの状況です […]
差分算は羊羹とエレベータ!君は数と友達になれるか?
Yahoo知恵袋で下記のような質問がありましたので初めて回答しちゃいました。(笑) それにしても、次から次へと質問があるのは分かりますが、投稿されて30分ほどなのに回答がどんどん入って来てるみたいで驚きました。 あれって […]
【帝都中学への算数】資料07:通過算を無理なく通過する
【帝都中学への算数】に「資料07:通過算を無理なく通過する」を追加致しました。 こちらは、1995年より企画したFAX塾に集まった小学生が、結局私の元に通い詰めることとなった際に、指導用のレジュメとして配布した資料の一つ […]
つるかめイチロー算と面積図のワナ!
↑OPEN ACCESS(PDFファイル24ページ)公開終了↑ 6月4日:OPEN ACCESS公開中(PDFファイル) つるかめ算は、「全部がツルだったら」あるいは「カメの足が2本だったら」という仮定をして、「でも実際 […]
幾何解きはピタゴランチのあとで
先般、幾何の問題の超初歩的標準問題の質問に対する解説を書いている中で、ピタゴラスの定理の本意に行き当たりましたので、合同や相似という幾何のabcを眺めながら、ピタゴラスの定理を通して幾何の苦手意識を克服してもらうきっかけ […]
6のパワー~算数のセンスは当たり前のことをするかどうか~
6×6×6×6×6×・・・・×6×6という計算があって、数えてみると式には6が666個ありました。 とても計算できませんが、この計算結果の十の位の数字さえ分かれば、世界のために大変役に立つことに利用できるそうです。 さて […]
何故ルート√を勉強しなくちゃいけないの?
このように尋ねられると、尋ねる人の真意というものがいろいろあって答える方も難しいんだね。 だから、対話しながらどういう角度から答えてあげるのがいいのかっていうことを絞りながら答えるのが本当は一番いいんだと思う。 とは言っ […]
六甲学院中学~算数:過去問で基本を鍛える(1)
本ページは「算数の基本を鍛える」カテゴリーでは、甲陽学院と並んで、東大寺学園・ラ・サール・武蔵中学etc以上にアクセスの多いページです。 やはり、私自身が六甲学院の出身だということが要因としてあるのかもしれませんR […]
東大寺学園中学~算数:過去問で基本を鍛える(2)
東大寺学園中学過去入試問題より・・・場合の数 いつぞやから新興(といってもかなり経ちます)の西大和学園の陰に隠れてしまっていますが、依然として奈良県きっての名門進学校です。 偏差値も西大和学園よりも若干高いようですね。 […]
青山学院中学~算数:過去問で基本を鍛える(3)
青山学院中学過去入試問題より・・・意地悪な人口密度 関東の学校事情には不案内ですが、なるほど算数には定評のある青山学院中学の「解けそうで解けない」問題は健在のようです。 悪く言えば「いけずな」・「意地悪な」、よく言えば「 […]
真和中学~算数:過去問で基本を鍛える(4)
真和中学過去入試問題より・・・錯覚を呼ぶ平均速度 全国的には馴染みのない名前かもしれませんが、熊本県の仏教系中高一貫私立の雄のようです。 私などは、熊本と言えば、高校として熊本高校と濟々黌高校が思い浮かぶ程度でした。 今 […]
ICL学院中学~算数:過去問で基本を鍛える(5)
ICL学院過去指導問題より・・・言い換える妙技 ICL学院中学校??…そんな学校ございませんm(__)m。 当【帝都大学へのビジョン】が約20年前に指導した小学生のために作った問題です。 自動機・産業用ロボッ […]
開成中学~算数:過去問で基本を鍛える(6)
開成中学過去入試問題より・・・難しそうに見えるけど 知る人ぞ知る開成中学 僕が大学を卒業した後から、開成が灘から東大合格者数トップの座を奪ったというニュースが流れたんだけれど、「そもそも生徒数が3倍弱ほども違うじゃん!違 […]
甲陽学院中学~算数:過去問で基本を鍛える(7)
本ページは「算数の基本を鍛える」カテゴリーでは、六甲学院と並んで、東大寺学園・ラ・サール・武蔵中学・灘etc以上にアクセスの多いページです。 やはり、近畿圏はかなり私学志向が強いということを反映しているのかもしれません。 […]
大谷翔平選手と81(9×9)マス曼荼羅チャートと勉強法
大谷翔平選手が大成した秘密として81マス曼荼羅チャートが挙げられますが、勉強法にも適用できるでしょうか?本当のことを言えば、大谷選手のように自分でマスを作り自分で埋めることが本当のスタートラインに立つことなのですが、それは、今までやる気がなかった人が意を決して全体のプラン設計図を立案するステップなのです。
脳に叡智を! | 学力低下の裏に潜むものから
『教育とは、学校で習ったすべてのことを忘れてしまった後に自分の中に残るものをいう。』『自分の中に残ったもの』とは何でしょうか?端的に言えば、誰にとってもは因数分解や二次関数そのものが大事なのではなく、これらを理解しようとした君たちの脳の軌跡こそが、自分自身や社会の裾野を作っていくということでしょうか!それこそが、『叡知』という一言で表せるのではないでしょうか?
物理の天才を閃かせたバルマー先生 | 数学脳への導火線 | 公開講座2
本講座は、誰も書かなかった、誰も教えなかった「数学が実際に使われた現場の再現ドラマ」です。 アインシュタインとともに20世紀の2大天才と言われたボーアの量子論の閃きは、実はスイスのバーゼルで中学の先生をしていたバルマー先 […]
ある朝、目が覚めたら秀才になっていた!あなたにもバイロンの奇跡は起こるのか?
ある朝、目が覚めたら秀才になれる予感がした。思わず、これを叫ぶようになれることは、1週間もあれば可能ですし、1,2ヶ月もあれば、実際の定期テストの結果として形に現れるところまで到達することができます。但し、何も準備していなければこの言葉は語れません。いつもの延長上ではなく、何か新しい試みでインパルスを与えないことには、しかも理に適っていないことには手に入れられない手応えなのです。
私立文系の数学選択と将来の年収
「学歴優遇」とは別に、「数学選択優遇」は就職の際に確かに存在し年収の差となって現れるという現実的メリットは論理的に物事を考える能力、論理的にものごとを積み上げていく習慣がついている、という評価を与えられることに現れます。
美しい日本の私~現代文・英語・社会をはじめとする勉強のススメ
川端康成がノーベル賞受賞講演で語ったように「祖に逢うては祖の脛をかじり」では、何事をも修めることは出来ないと心から理解できたとき、人は必ず成長するのです。「禅でも師に指導され、師と問答して啓発され、禅の古典を習学するのはもちろんですが、思索の主はあくまで自己、悟りは自分ひとりの力でひらかねばならないのです。」という川端の言葉を「勉強でも師に指導され、師と問答して啓発され、勉強の常道を習学するのはもちろんですが、学ぶ主はあくまで自己、本質の理解は自分ひとりの力でひらかねばならないのです。」という言葉に置き換えて考えてみられては如何でしょうか?
ことばのあや~国語の素養
「ことばのあや」は、表現の美しさ・巧みさを目的とした修辞法であり、文章やことばの飾だったが、次第に言い逃れやごまかしのテクニックとなってしまった現在。国語学者であった故永野賢氏の『国語の素養』を通して、「ことばのあや」や「韻を踏む」ということの本来的な意味を見つめ直し、現代文を通して、言葉の持つ意味や重さを考えるとともに、さりげない教養を身に着けてほしいと願います
丸竹夷二押御池~場合の数とは? | 数学脳への導火線 | 公開講座1
本講座は、小学5年生と高校生の両方に向けて指導資料としたものです。 当時はwindows95の時代で、私もCADでしかPCを使っておらず、ワープロも一太郎の方が使いやすいなと思っていたこともあり、資料は手慣れたCanon […]
河盛好蔵『Bクラスの弁』~分に甘んじて、しかも心腐らず
自己の能力と他人の才能に対する正しい判断や評価のもとに、分際をわきまえ、Bクラスの勉強・仕事を黙々と積み重ねるところに充実した人生があり、そのことによってAクラスへの道が開かれることがあれば、それは思いがけないラッキーとして受け入れるほどの気持ちが大切です
自分の手で、爪に血をしたたらせて、こじあける
どんな分野に進むにしろ、普通の一般社会に出るにしろ、自分たちが羽生選手になれるはずもないからといって、何もこじ開けようとしないのであれば、それは正しいことでしょうか?そして何より自分の人生にとって何らかのメリットがあるでしょうか?器の大小には関係なく、世間の甘言に惑わされることなく、努力するということ自体が尊いという気持ちを出発点とされてください。
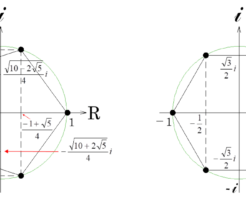
正多角形と方程式 \(x^n-1=0\) の不思議な関係
正三角形と方程式 \(x^3-1=0\)、正方形と方程式 \(x^4-1=0\) 複素平面(ガウス平面)に、実数の1を起点として、単位円上に正三角形と正四角形(正方形)を書きます。 「それがなんなん?」と思うかもしれませ […]
American dream no more contented but frustrated~受験英語 勉強の仕方例講座02
次の英文を日本語に訳してみよう!【今日の課題ノート】 We have now virtually accomplished this first American dream. We have achieved mate […]