「知っ得で知っ解く二次関数(放物線)」目次
実は、因数分解と二次関数と二次方程式は濃い親戚のようなものなのに別々に習わされることは仕方ないとしても、誰もその間柄を「あっ、そういうことなのか!」と思わせてくれるような説明をしてくれないから、公式を覚えることに必死になっちゃってチンプンカンプンになっているだけ!
二次関数が絡まないような問題はないと言っていいほど数学の血液のような単元ですから、ここさえ全体を見渡すように鳥瞰できれば、一挙に難関大学の下位合格者ぐらい押しのけちゃうことができます。
最初に申し上げておきたいことは、高校数学で成績が伸び悩んでいる人は、必ず二次関数の本質が全然理解できていません。
難関大学の理系ですら、暗記しているだけで処理しかできない人も昔から結構沢山います。
公式を丸暗記しているだけで、因数分解・二次方程式やそのいくつかの公式と全く線で繋がっていないことだけは確かです。
逆向きに言えば、点と点を線で繋げて意味を理解していれば、公式なんてほとんど覚えようとも思いません。
ただ、いくつかの問題と向き合っている中で、結果的に勝手に感覚で覚えてしまっているだけです。(仕事をしていたら誰でも勝手に覚え込んでますよね!)
全79ページ
- ●夏期セミナー:二次式・二次方程式・二次関数を体系的に理解する(超初級) 4~
- ~優等生でも意外に分かっていない体系~
超初級の目線で、【因数分解】【解の公式】【解と係数の関係】【軸の位置】【判別式】お互いの血縁関係の全体図をザっと掴んでいただきます。
なんと、たすき掛けの正体から始まり、平方完成することとフリーハンドでグラフを描ける重要性をまずはお話しします。
- ●第1章:二次関数(放物線)を見渡す風景 19~
- ~姿が変わると血縁関係が見える~
二次関数(放物線)を東西南北4か所に設置した定点カメラで眺めてみると、【因数分解】【解の公式】【解と係数の関係】【軸の位置】【判別式】お互いの血縁関係が面白いように分かります。
- ●第2章:二次関数(放物線)と二次方程式 25~
- ~解の公式と判別式~
判別式は解の公式の√の中身。
その中身がマイナスになれば君はうろたえる。
そのうろたえるうろたえないが解の有無の判別基準になるだけのお話。
- ●第3章:二次関数(放物線)をグラフで捉える 27~
- ~放物線のグラフは軸の位置が生命~
「二次方程式は二次関数:y=(xに関する二次式)とY=0の連立方程式」なんてことすら気付いていない子も多い。
それさえ理解しておけば、二次方程式も判別式も全てイメージで理解できます。
西側から眺めた風景で、軸の位置・頂点の位置をしっかりイメージで掴むことの訓練こそ最重要!
- ●第4章:二次関数(放物線)を確定する脳細胞たち 30~
- ~二次関数をスマートに確定する現場~
『xに関する二次方程式f(x)=0の解は2と3である。この時、y=f(x)の軸を求めよ。』
東君と西君の脳細胞を比較しながら、瞬間解答できて当たり前の脳に君を導きましょう。
- ●第5章:一次関数(直線)を見渡す風景 33~
- ~二次関数よりシンプルな血縁関係~
二次関数も一次関数や円との絡みで問題とされることが多いから、一次関数を同様に全体を見渡しておこう。
- ●第6章:一次関数(直線)を確定する脳細胞たち 34~
- ~一次関数をスマートに確定する現場~
東君と西君の脳細胞を比較しながら、よりスマートな脳に君を導きましょう。
「東には東の正しさがあると言う。西には西の正しさがあると言う。」君はどちらが好き?
- ●第7章:切れ味抜群!交点をめぐる「知っ得」風景 37~
- ~脳の切れ味とはこういうことを言うのです~
一次関数(直線)、二次関数(放物線)、円を巡る交点の問題は、それぞれの見える姿を上手くチョイスしたり、ある真実を使うことで、とてもシンプルに処理できてしまいますま。
- ●第8章:発展問題6題 45~
- ~発展問題6題~
さぁ!「二次関数って意外に簡単じゃん!」そう感じてみましょう。
「知っ得で知っ解く二次関数(放物線)」特徴
- ■全体を見渡すことで・・・
-
君の頭の中は、公式だけが孤立して存在していますね。
二次式・二次方程式・二次関数を体系的に理解することで、ややこしそうな公式の繋がりがイメージで見えてきます。
バラバラに暗記しようとしていた時の時間の浪費や精神の苦しみから、どれほど解放されることでしょう。
その関係性さえ掴めば、君は一気に「数学」を呑んでかかることができるようになります。
- ■東がスマートか?あるいは西がスマートか?
-
頻出の交点を求める問題、あぁ、嫌だ嫌だ!
直線、放物線、円の方程式の確定の仕方、これらの交点を巡る方程式の確定の仕方。
東西南北から見えるどの姿で処理してやれば最適なのか、現場に臨場して、その妙味を盗んでください。優秀な講師なら、注力して指導する部分ですが、その辺りの塾ではポイントとしてすら教えれる講師が居ないでしょう。
- ■分かりやすい例題に脳細胞の動きを散りばめると・・・
-
式だけで処理していたら嫌になるのは当たり前!
たいていの参考書の解答例は、図は示してあっても、何故そうなるのか?を省略している場合も多々あります。
だから読んでも何かが足りない!?概念を理解する上での分かりやすい例題を、出来る限り豊富な言葉で、脳細胞の働かせ方から語ります。
- ■ガリレオが、実際に高校生を指導し、成績をアップさせたエキスを集大成
-
数学苦手の子が、いつしか苦手意識を克服した!
少数だけれど、軒並み教え子の成績をアップさせたガリレオならではの手腕が今ここに蘇る!
- ■ロマン心を呼び覚ます「天才ボーアを閃かせたバルマー先生」
-
二次関数なんて勉強して意味があるの?
申し上げておきますが、今君たちが享受している文明の屋台骨は二次関数と三角関数です。
これらなくして、現在の文明は成立しません。そんな二次関数の現実社会での威力を、未だ、誰も書いていないと思えるユニークな切り口で面白くストーリーにしました。
現実の学者さんたちの脳はこんな風に働いていることも想像していただけます。
海城高校の過去入試の問題ですが解けますか?
-良問ピックアップ | 2020年4月度-
中学生にはなかなか難しい問題だと思いますが、れっきとした海城高校の過去入試問題。
大学受験生の君であれば解けるはずですが、如何でしょうか?
【問題】
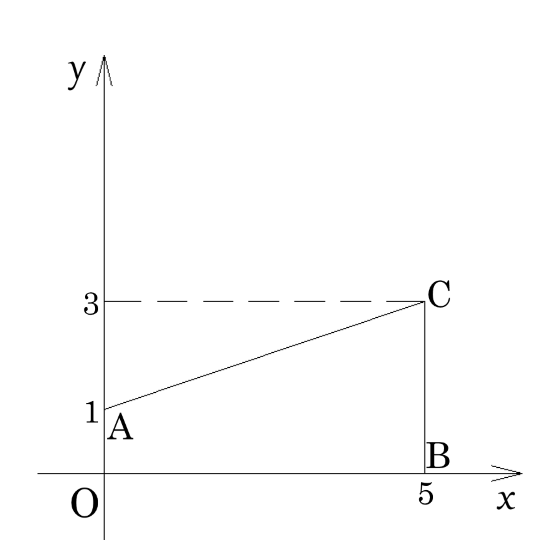
2次方程式 \(x^2-5x+3=0\) の2つの解 \(p,q\) をx軸上に \(P(p,0),Q(q,0)\) となるように作図することにしました。
\(A(0,1),B(5,0),C(5,3)\) とし、\(A\)と\(C\) を結び、最後に何かをして図は完成しました。
- 最後に何をしましたか?
- \(P,Q\) の位置はどこになりますか?
この問題の着眼点がすぐに見つけられるようであれば、君は二次関数の様々な概念の本質をちゃんと日本語で掴みとっていると言えるでしょう。
実際、この問題は、本図を見ながらと教科書に載っている放物線のグラフを思い浮かべることだけで、日本語だけでシンプルに説明ができますし、君も説明を聞けば、「そんなことなら知ってたのに…」と呟くことでしょう。
しかし、公式を式だけで覚えている場合には、何から手をつけていいのかが全く浮かんでこないでしょうし、説明を聞いても本当には理解できていないと思いますよ。
知っ得で知っ解く二次関数(放物線)の仕上げ問題
本資料を読み、丁寧に理解を進めていかれると、問題集や参考書の標準問題程度は面白いほど解けていくことでしょう。
数学が苦手な君であれば、これらを解く際に、本資料を横に置かれておいて対照しながら進めることで、今までして来た何気ない勉強よりは数倍の達成感が実感できる筈です。
そして、本資料の最後にある発展問題(難問ではなく、本質をえぐり出すための問題)も、着眼点とアプローチを脳細胞の働き視線で記していますので、これをじっくり理解し、翌日に自力で再現出来ようものなら、もう何の心配もいりません。
仕上げとして以下の6題にチャレンジしてください。
当然、脳細胞の動きに則した解説と解答も記載してあります。
講座をしっかりと読んで噛み締めてくれたならば、かなり自力で解けていく実感を味わえるでしょうし、もし躓いたら講義の部分と対照しながら噛み締めていくと、なお一層強固な実力を付けていくと思いますよ。

物理学の有名な方程式だって数Ⅱ数学のレベルで導き出せます!
「知っ得で知っ解く二次関数(放物線)」は、「因数分解や二次方程式と結びつけて理解することで実に簡単に理解できるんだよ!」ということを感じてもらうための語り部として、参考書・問題集では省略され、決して見えない部分までを、図で理解するA4トータル79ページのボリュームにまとめ上げました。
こんなコンセプトでも、バルマー先生のお話を入れても、たった79ページにしかならないほど、実は簡単な単元だったんですね。
なのに、数学の血液とも言える単元であり、現代物理を説明する立役者なのですから、ちょっとしたきっかけだけで、君は物理学者の道を歩み始めるかもしれません。
有名な予備校や塾でもまず出会えない講義
その証拠に、量子物理学の天才ボーアが唸ったバルマー系列の数式を、その時代に産まれていたとすれば君が発表したかもしれないことを主題とした「天才ボーアを閃かせたバルマー先生」PDF(16ページ)を結合し、計79ページでご提供しましょう。
世間は広しと言えども、不思議にも、まだ誰も書いていない切り口です。
有名な予備校の講師さんですら、こういった切り口で教えることなど考えたこともないでしょうし、ましてや実社会の大多数を占める平均的な指導者レベルでは、巡り会えるはずのない切り口です。
これを読んで、平凡だった子が学者を志すなんてこともあるんじゃないかなと密かに思っています。
知識が体系化されれば、これだけでも難関校にも行けちゃうぐらい
変な言い方ですが、中学受験の少し難しい問題を考えれるぐらいの力をつけた後は、因数分解と三角関数と二次関数を理解して実践訓練しておけば、普通の一般社会ぐらいなら悠々と渡っていけます。
そして、文系でもここは突破するぐらいの理解力と思考力を養っておかないと、「一事が万事」、言われたことは出来ても自分で企画が出来ない人材になってしまう可能性はより大きくなると思います。
この資料は、「苦手・出来ない・分からない」を一転、難関大学レベルに仲間入りさせるためのものであって、平凡で不器用な子にこそ、暗記だけで受験を突破する優等生に替って合格していただくため、そのきっかけ作りになってほしいと願って書いています。
また、平易で緻密な語り口の講義をそのまま文章化したかのような資料ですから、講義のように言葉が宙に舞って消えるだけで終わりということもありません。
資料の最後に付属している問題(発展6題)は、
- 本質をえぐり出すような問題
- 標準からやや背伸びを要する問題
とは言え、出来たからと言って「凄ーい!」というほどでもないレベルですが、理解を深める良問です。
もし、なぞって理解出来るのであれば、君は難関大学だって射程距離に入れる可能性が十分にありますから、難関大学へトライできるかどうかのバロメータにしてくださいね。
もし、実力テストとして使ってみようと思う方は、問題だけが書かれたページがありますから、そのページを印刷して60分を目途にテストのつもりでトライしてみてください。
また、本資料は、
- 行き詰まった時
- 何故そうなるのかが腑に落ちない時
引っ張り出してきて、該当部分を読んでいただくことで、霧を晴らして頂くような使い方に最適です。
数学の出来不出来の格差をつけてしまうのは、
やはり「二次関数を体系的に把握する能力」
この能力を中途半端にしている限り、
この能力を甘く見ている限り、
この能力から目をそらしている限り、
全ての単元において一定の壁を破ることはありません。
難関大学へ繋がる数学
難関大学へ繋がる数学の勉強の仕方は、ひとえに最上流の単元を曖昧にしないことです。
とりわけ、「数と式」「二次関数・二次方程式」「三角関数」は全体を流れる血液のような単元!
これらさえものにすれば、
- 本番入試においても50点は取れる
- 自ずと他の単元も面白いように捗る
ようになるほどの代物です。
後は、必ず1問は出る「確率・統計」をしっかりものにしておけば、75点が取れるということです。
大学の独自入試で数学75点ではご不満ですか?