
本記事は、お子さんが文章題(算数)が苦手だというお悩みをお持ちの保護者さんが指導の参考にして頂けることも視野に入れ、数学がジリ貧であることに悩む中高生向けとしても有用として執筆しました。
最終的に、文章題を解く上でのポイント要素を、具体例で説明させていただいておりますので、楽しみに読み進めてください。
保護者さん自身が楽しみながら、子どもさんにより的確なアドバイス、子どもさんを伸ばすアドバイスをしていく醍醐味を感じて頂けるのではないでしょうか?
文系に進む人は、みんな数学が得意なの?
「国語が出来れば文章題(算数)が出来る」という論があります。
あるいは、「文章題(算数)が出来ないのは国語力がないから」という論があります。
私も、学生時代に論議を尽くしましたし、文章題をこなす上での基本要素であり前提の一つであることには何も異存はありませんが、それでも、一概には言えないと以前から書いています。
一つお断りしておかねばならないことは、ここでは「問題文が理解できない」という読解力面での「文章題が解けない」というお話ではないということです。
読解力レベルの悩みにまで到達していれば「算数の問題文が理解できない」などはあり得ません。
適性検査の長文ならまだしも、普通の算数の文章題で問題文が理解できないというのは、国語という一つの側面だけで見ても、読解力以前の「言葉を理解する力」「言葉を扱う力」「基本的な日本語力」の欠損であって、読解力を持ち出して対策できる問題ではありません。
そういう意味で広く「国語力」という言葉で語られるわけですが、それとて、この言葉だけの丸投げでは、単に一面的な要素を抽出しただけのものであり、とてもとても「文章題ができないのは国語力の無さだ!」「算数ができないのは国語ができないからだ!」などのタイトルは恥ずかしくて付けれるものではありません。
「読解力」とセットで語られるのみの記事があれば、なお一層、愚かなことです。
もし、読解力の意味を期待されておられるのであれば、文章題の得手・不得手とは焦点が合いません。
そもそも、単に算数の文章題の得手・不得手を「国語力」や「読解力」に帰着させてしまうと、世の中の傾向としてある「国語や社会はそれなりにできるけど、数学や物理ができないので文系に進む」なんて現象の説明にも矛盾が生じますよね。
さて、私たちの勉強法書や算数・数学の資料類、ブログを読まれたらお分かりいただけると思いますが、「日本語で・・・」という文言が頻繁に使われているはずです。
この「日本語で・・・」を通して、一般論で飛び交う安直な「国語力」なる言葉を見直しされると、視界がくっきりとしてくると思います。
読解力の本質に関しましては、むしろ、以下の記事の方が相応しいですので、ご一読ください。
読解力を鍛えるとは? | 7回読み・10回読みなどに惑わされないこと
最初の素材問題はこちら
![]()
【問題】
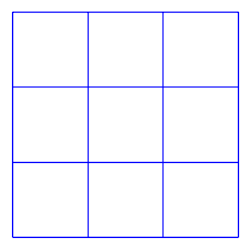
右のマスに、1から9までの整数を1つずつ入れて、縦に3つ足しても、横に3つ足しても、斜めに3つ足しても、その和は同じになるようにします。
- (1)同じになる3つの数の和はいくらでしょうか?
- (2)真ん中に入る数は必ず5であることを説明してください。
「どこが文章題だよ?単に、魔法陣じゃん。」と、ご不満に思われるだろうことは承知の上です。
ただ、ここでは、どんな文章題でも日本語を数学後に変換する感覚を掴んでいただきたいという意図があることをご理解の上、読み進んでいただければ幸いです。
何故、こんなことが今まで出来なかったのだろうか?
君たちの中には、文章題が苦手だという諸君はたくさん居ると思います。
あるいは文章題になると出来ないという諸君もたくさん居ますよね。
そこで、「どうすれば文章題がこなせるようになるのか?」というテーマを考えてみたいと思うわけですが、テーマが文章題だからといって、小学生だけに関する課題ではないということを、まず前置きさせて頂きますね。
中高生で数学が苦手だ、できないという子は、たいてい、小学生の文章題を解こうとしてみても、小学生の頃に手が出なかったのと同じぐらい手が出ないことも多い筈です。
下手をすれば大人になっても文章題が紐解けないケースはあちこちで見られるのではないでしょうか?
実は、数学が苦手とか嫌いだという高校生も、むしろ小学生の文章題をじっくり考えて攻略してみようとする類の試みを忘れて、目先の数学を課題消化的に嫌々こなすだけでは、結果的にワンランク上のステージに立てる可能性を潰しているとさえ言っても過言ではありません。
何故なら、文章題をこなすには様々な要素の能力が揃わなければならないからです。
そして、算術レベルの文章題をこなすための要素を揃える準備は、少なくとも小学校の時よりは年齢相応に十分にできている筈だからです。(あくまで「準備」ですよ!機能させて来なかったのですから..)
この要素がどういったものであるかは、この後に明らかにしていきますが、大切なことは、これらの要素を機能させることであることを忘れないことです。
機能は先ず動かせ始めないと、その動きを延長することも拡張することもできません。
機能を起動させようとする努力は、必要となる知識が難しい段階で試みるよりも、より易しい段階で試みる方が実を結びやすいのは理の当然ですね。
そういう意味でも「脳細胞を働かせてちょう題」や小学生の算数をコンテンツにしているわけです。
そして、実を結びさえすれば、本人自身が、「何故、こんなことが今まで出来なかったのだろうか?」と不思議にさえ思え、一挙に霧が晴れたことを感じるのがパターンです。
普通の大人に限らず、立派な数学者でさえ、算数の文章題をこなせる要素が出揃って、一挙に霧が晴れた瞬間こそを自分の誕生日だったと振り返るのではないかと思います。
ですから、高校生だからといって小学生の文章題を解くことを恥ずかしがることはありません。
一昔前ならともかく、今では、むしろ解けない方が普通なのですから…。
小学生の文章題が紐解けない内は、今習っている数学がじり貧になることはあっても伸びるようなことは決してありません。
しかし、小学生の文章題が紐解けるようになったとき、一気に来ます!
小学生の文章題でなく、今やってる高校数学でも来る子は来ます!
数学に向き合うコツが一気に分かり出す時が…
その時が来る時期が違うだけです。(何も働きかけがなければ、とりあえず今日も来ませんが…。)
ですから、小学生のお子さんを指導する保護者さんは、むやみにキーキーがなりたてることは、その時期が来るチャンスをも奪うことになりかねません。
何も働きかけをしなかった方がよかったなどという結果に終わらないように、それだけは肝に銘じておいてください。
ともかくも、攻略できた時の感覚はもちろん、答えに近づいている感覚を知覚したときに、一挙に霧が晴れてくる感覚と同時に面白いと感じる感覚がやって来ます。
出来る子は必ず、そういう瞬間を味わっています。
国語が出来れば文章題(算数)が出来るの?
本論に入る前に、一つ前置きをさせて頂きます。
- こうすれば文章題がこなせるなどという一意的な答はないということ
- 敢えて答を出せというなら、答になるかもしれない沢山の準備はあるということ
- よって、答が出る時期は人によって違って当たり前ということ
ここを押さえておかないことには、大きな過ちを犯してしまうかもしれません。
「何故、文章題が苦手なのか?」という問には、様々な議論がし尽くされていると思うのですが、確かに言えることは、どの主張も一概には言えない一面だけを採り上げて仰々しく宣伝しているものばかりだということです。
「国語が出来れば文章題(算数)が出来る」という論があります。
私も、学生時代に論議を尽くしましたし、文章題をこなす上での基本要素であり前提の一つであることには何も異存はありませんが、それでも、一概には言えないと以前から書いています。
国語が出来るだとか、本が好きだとか、読解力があるとかだけでは荒っぽ過ぎるんですね。
実際に「国語が出来る子は算数も出来ていますか?」と問えば分かりますね。
一概にそう言えないことは周囲を見渡すだけで一目瞭然ですよね。
もっと言えば、「本が好きでよく読む子は算数ができますか?」
一概にそうは言えません。
それどころか、本を読まない子がスラスラと解いたりする例はいくらでも知っています。
但し、この場合の「本を読まない子」というのも、普通に日本語が理解できているという前提が含まれています。
何も、国語の成績が優れている必要などなく、普通に分かっているというだけでいいのですが、その前提は確かにあります。
ところが、昨今はその前提自体が危ういという状況のように見受けられます。
「言葉を理解する力」「言葉を扱う力」「基本的な日本語力」自体が危うい状況です。
この視座でのお話は、前述しましたように、下記ページをご一読くださいませ。
読解力を鍛えるとは? | 7回読み・10回読みなどに惑わされないこと
上の「読解力を鍛えるとは?」の冒頭でご紹介した朝日新聞の記事ですら、リーディングスキルテストの結果を「教科書の文章、理解できる? 中高生の読解力がピンチ」などというタイトルを付けているのですが、これこそ「読解力」以前の問題です。
かと言って、「言葉を理解する力」「言葉を扱う力」「基本的な日本語力」といった「国語力」だけに帰着することもできない他の原因を多く孕んでいます。
コーヒーブレイク
ある意味、私自身が別に本が好きでもない代表選手でしたから、「国語」という観点から見れば、こと文章題に関しては、普通に日本語が話せ、理解出来ればいいと考えています。
中学を卒業して高校に入ってから、ようやく評論を主に、文学では太宰、芥川、坂口、公房などに限られますが、読むようになった程度です。
下の画像は小学校卒業時に灘中学と甲陽学院中学に進学したクラスメートからのメッセージです。
後者は、テーマとはあまり関係がありませんが、ちょっと気分転換に、ざまねぇ奴だったんだと笑い飛ばしてやってください。


とは言っても、文章題を解く力に国語の勉強や本を読むことが一概には依存していないからといって、無視をしていいというわけではありません。
本が好きでも、本をスラスラ読めても純粋に理解が出来ていない場合すら想定されますので、これではやはり困ります。
と言うか、文章を読んで、その内容を理解するという、一般的に「読解力」と呼ばれる能力自体はあらゆる成長の根幹を担う部分であって、文章題に対しても微少とはいえ同様だということです。
ただ、「言葉を理解する力」「言葉を扱う力」「基本的な日本語力」が欠損していれば、それ以前の問題であり、
ですから、損得で考えるようなことではなく、その努力や働きかけは常に心掛けていくべきものです。
一方、算数の文章題に限れば、本人の中では理解はできているけれど表現が出来ない、あるいは表現する方法を知らないのであろうと思われる節も、教えていると多々あります。
国語のように純粋に「読解力」だけを抽出してテストすることは、算数では難しく見えにくいのです。
よく見ていると、文章問題を読んだ後、たいてい、ピタッと動きが止まります。
意味が分からずに動きが止まる場合、意味は分かっているけれども動きが止まる場合。
前者は読解力の問題ですが、後者は読解力の問題はクリアしています。
動きが止まって1分、2分・・・微動だにしない。
まさにこの時、「それって、どういうこと?」「別の言い方をすればどういうこと?」って働きかけをしていくことになるわけですが、たいていは、算数であるという特殊事情が表現することをためらわせていることの方が多いことに気付くことになります。
総じて、算数の文章題に限れば、私の経験からは、文章が長文だったり、入り組んだ構造をしたような場合を除いては、純粋に読解力がネックになる場合よりも、そこから先がネックになっている場合の方が多いと分析されます。
文章題を解く立役者とは?
ここで、文章題を紐解くにあたっての全体的な流れを、必要な要素で区分けする感じでまとめました。
流れ図と言っても、それぞれの領域は一方通行だけではなく、行きつ戻りつで確認や修正をしながら進むと考えてくださいね。
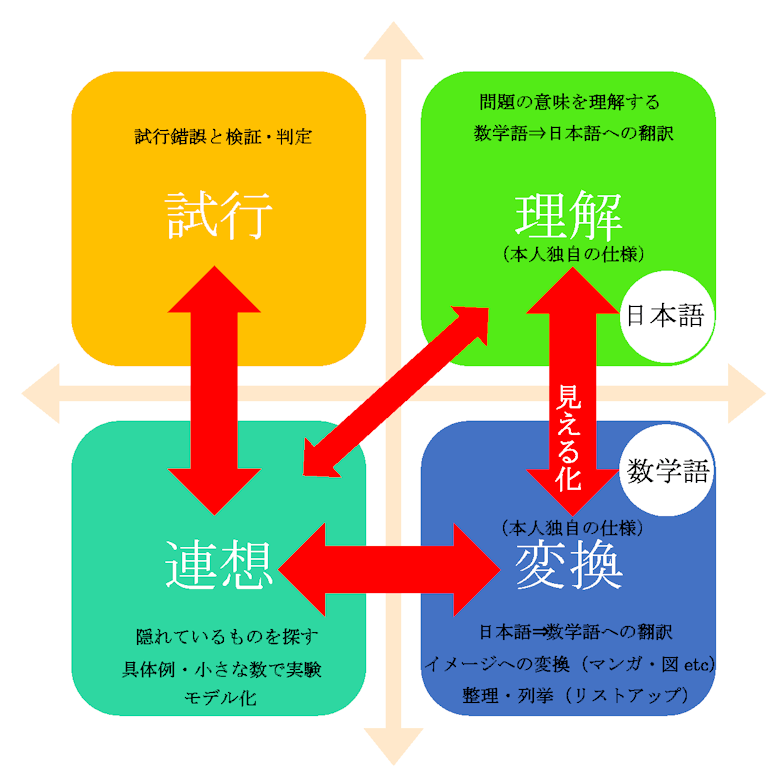
簡単に説明しておきますと、
- 日本語(文章)を読み意味を理解:各人独自の仕様で意味を理解します
- 理解を算数語に変換:マンガや図や式、箇条書き等として各人独自の仕様で見える化
- 答に繋がる道筋を連想する:具体例や小さな数で実験をするなどで道筋を立てる
- 試行する:立てた道筋を実行し、上手く行かなければ原因を別法を考えるか判断する
といったイメージになります。
4つの言葉「理解」「変換」「連想」「試行」は、あなたが理解しやすい言葉に置き換えてイメージ化していただいて結構です。
文章題と言っても、その内容は様々です。
杓子定規にこの4つに分類するのは難しい場合もありますし、いずれかの要素を省略できる場合もあるでしょうから、最大公約数的な要素分類と考えてくださいね。
さて、文章題に共通しているのは、何をすればいいのかを導き出さなければならないことです。
そのためには、問題は何を意味しているのかを、一目で見えるようにしなければなりません。
計算問題のように、手続き通りに処理していけばゴールに到達するものではありません。
ネズミが学習によって同じことを反復することが出来るようになるのとは性質が違うというわけです。
習慣や条件反射で反応するのではなく、「理解し、考えて判断する」という要素が必須になります。
小学校高学年で九九が出来ない子はいても、大人になっても九九ができない人はほとんど居ないですよね。
九九が出来ないと、何より普通に生活する上でも不便ですから、実際に使うことで自然にできるようになります。
「見える化」ができる準備を粛々と
しかし、文章題は少し様子が違って来ます。
習慣や条件反射でいつかは出来るようになるものではありません。
「理解し、考えて判断する」という要素が無ければできないことなのですが、この能力を発揮するためには必ず何らかの準備が必要だということです。
即ち、「何らかの準備」は文章題を解くための準備というだけではなく、「理解し、考えて判断する」という能力全般への準備ということになります。
そして、この準備は、単に読解力だけではなく、日常的な常識でもあり、考えてみようという気持ちの芽生えでもあり、これをサポートする周囲のアドバイスの的確さでもあります。
これらがバランスよく準備できた時、初めて「理解し、考えて判断する」力に水分を送り始めます。
その中でも、君自身が意識的に努力すれば一挙に準備が整いそうな極めつけの要素が「変換」=「見える化」です。
算数の文章題を解ける子、解けなくても答えを進めていける子は、
- 意味を考えて理解しようとする
- その理解をするためにもイメージとして表現したり、書き出したりする作業をする
- そのイメージを利用することで、道筋を考えたり連想がしやすくなった状態で試行錯誤を繰り返す
と、上の流れ図のように進めていくのですが、アンダーラインを引いたように、「変換」=「見える化」は理解や連想をも刺激する優れものだということを忘れないようにしてください。
お待たせいたしました。
では、実際の問題を進めながら、その感覚を体験しみましょう!
文章題を解くための一つのモデル
【問題】
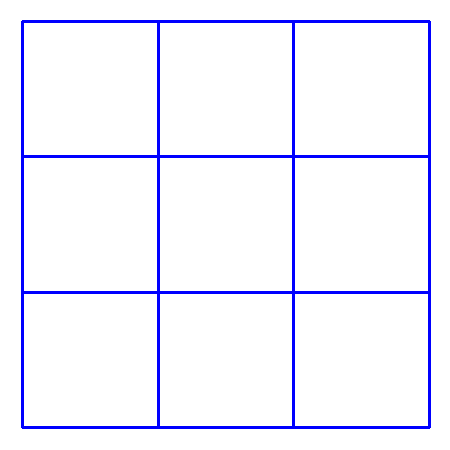
右のマスに、1から9までの整数を1つずつ入れて、縦に3つ足しても、横に3つ足しても、斜めに3つ足しても、その和は同じになるようにします。
- (1)同じになる3つの数の和はいくらでしょうか?
- (2)真ん中に入る数は必ず5であることを説明してください。
まず、自力ででこの問題の解決に向けて頑張ってトライしてみてください。
お母さんやお父さんも、お子さんによりベストな指導をするためには、頑張ってトライしてくださいね!
ここまで、君のペンは動きましたか?
何かを書き始めましたか?
問題のマス目を眺めているだけだった君は、虚しく時間が過ぎていくだけだったですね。
さて、問題に書かれている文章は9つのマス目に関する内容だけですから、その内容をマス目上で表現する以外にはすることがありません。
本問の場合は、最初からマス目というビジュアルが与えられていますけれど、何もビジュアルな対象が与えられていなくとも、問題の全体を捉えるためには一目で見て分かるビジュアルなイメージにしておくことが重要です。
特に算数の文章題の場合には、マンガや図形や式として表現できるものはする、あるいは、沢山のことが書かれている場合には全て書き出すなどの作業があります。
ここは、前処理と呼ぶに相応しい、日本語から数学語への「変換」ステージになります。
「変換」という言葉がしっくりこなかったら「翻訳」でもなんでも構いませんよ。
先ほどの流れ図を見て頂いたときに、「連想」のステージが最も難関と思われたのではないでしょうか?
実際そうなのですが、実は、たいていの子はその前段階の「変換」のステージからできません。
この「変換」のステージが出来ないことが致命的なんですね。
何故なら、「変換」する作業をしている中で「連想」が生まれて来るものだからです。
では、作業を始めていきますので、教訓を一つでも感じ取ってください。
本問の場合の例として、私は次のような絵を描きました。
まぁ、一般的にはこんな絵になると思うのですが、平凡で面白くないと思われたらどんどん提案ください。
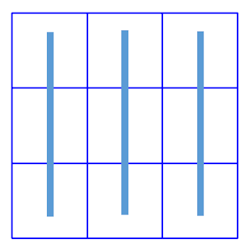
縦に3つ足しても
![]()
横に3つ足しても
![]()
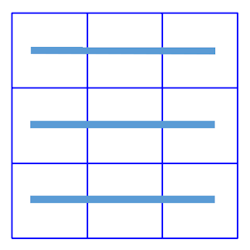
斜めに3つ足しても
![]()
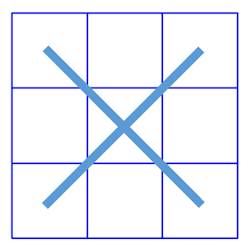
このぐらいであれば、ワーキングメモリー(作業記憶)領域の小さい私でも、実際に書かずとも頭の中で描いて処理できちゃうのですが、それでも描いておく方が何かと得策です!
このことは後で分かることになりますよ!
あなたは「説明なぞ要らない」というかもしれませんが、脳細胞が呟く言葉で解説だけしておきますね。
-
理解1:縦に3つ足す・・・3か所ある(3列)

変換1
それぞれの列に縦の線を引き、その線上にある3つの数字の和だと考えるぞ!
(線でなく、細長い楕円で囲っても構わない。)
-
理解2:横に3つ足す・・・3か所ある(3行)

変換2
それぞれの行に横の線を引き、その線上にある3つの数字の和だと考える
(線でなく、細長い楕円で囲っても構わない。)
-
理解3:斜めに3つ足す・・・2か所ある(対角線)

変換3
それぞれの対角に斜めの線を引き、その線上にある3つの数字の和だと考える
(線でなく、細長い楕円で囲っても構わない。)
これで、書かれている文章の内容はすべてマス目の中でビジュアル化されました。
これ以上、することは無さそうですね。
ここで、君は「右のマスに、1から9までの整数を1つずつ入れて」を表現していないよ!と言うかもしれませんね。
では、適当に数字を入れてみて次に進んでみてください。
- 縦に3つ足したらどれもが同じ数になりましたか?
- 横に3つ足したらどれもが同じ数になりましたか?
- 斜めに3つ足したらどれもが同じ数になりましたか?
まぁ、なっていないですね。
それなら、ただ混乱させるだけのようなものではないですか?
マスには、1から9までの整数を1つずつ入りますが、どこに何が入るかは全く分かりません。
こういった時には、「マスには1から9までの整数が1つずつ入る」と頭の中に入れておくか、今、あるいは後で必要を感じたら【a,b,c・・・】とか【ア,イ,ウ・・・】とかの記号で入れておけばいいんです。
問題を通して、こういった知恵を一つづつ身に着けていってください。
人の話を「なるほど!」と頷いているだけでは、絶対に身に着きませんが、考え、悩む作業さえしていれば必ず体で覚えていきますから安心して下さい。
さて、このイメージを見て、何が言えるのか?何を引き出してくるのか?
ここからが「連想」のステージになるんですね。
「連想」という言葉がしっくりこなかったら「考察」でもなんでも構いませんよ。
このイメージを眺めて、「それがどうしたの?」って思うだけで、それ以上進まなかったとすれば、「私は算数を解いているんだ!」ということを思い出してください。
この文章で算数であることを表している言葉は「足す」という言葉しかありません。
そして、3つの数字を「足す」ということを1本の直線で表現し尽くしました。
何かやり残していることはないでしょうか?
3つの数字を「足す」ことは表現しましたが、9つ全ての数を「足す」ということはしていませんね。
何故、気付かなかったのでしょうか?
一つのヒントを差し上げましょう。
縦の直線3本を1本ずつ、「足す~ 」と呟きながらなぞってみてください。
マス目の数を全部足してるじゃない!ってなりませんか?
もし、君が文章題の訓練をよくしていて、算数語やイメージに変換することに慣れていれば、おそらく、イメージを見た段階で、縦に引いた3本の線の中にはマス目の数が1回ずつ入っていることに気付くことでしょう。
横に引いた3本の線も同じことだと分かるでしょうし、対角の2本の線には含まれていないマス目があることにも気付いちゃうことでしょう。(気付かなくても全然構いません。)
何かに気付こうと考え悩んだ軌跡の数だけ、こういうことに気付く日は確実に近づいています。
この辺りから、「連想」→「試行」へと移っていくことになります。
「見える化」したからこそ、考えたり連想しやすくなっていることが分かりますか?
-
連想1:3本の縦線をすべて足す=9つのマス目の数字をすべて足すことだ!

3本の縦線はすべて同じ値である。⇒ 全体を3等分していることではないか!
全体とは9つのマス目の数字をすべて足したもののことだ!
-
試行1:全体(9つの数字の和)を求め3等分する

全体とは、1+2+3+4+・・・+8+9のこと!
(1+9)×9÷2=45→→→ここは分かるよね!
確かに3等分出来て、それぞれの縦線は45÷3=15理解2⇒変換2でやっても同じことになるぞ!
「連想」のステージで考えたことは、君の経験と体に刻み込まれることになり、それがどんな問題が来ても太刀打ちできる力となっていきます。
少なくない評論家は「パターンを暗記すること」と言いますが、そうではありません。
パターンを暗記しようとしてする勉強と真剣に考えた結果としてパターン認識の形で体に刻み込まれる勉強とは月とスッポンほど違うのです。
では、引き続いて「(2)真ん中に入る数は必ず5であることを説明」を考えていきましょう!
連想への協奏曲
- 【理解1⇒変換1】と【理解2⇒変換2】は縦と横が違ってるだけで、問題(1)の結論以上のことは出てこないじゃないか!
- ところで、【理解3⇒変換3】はまだ使っていないし、問題(1)の答は、ここからじゃ出せなかった!・・・ということは、これがクサいカモ!
- それに、なぜ、真ん中の数を尋ねるんだろうか?・・・この疑問が実に大切なんだよ。

【理解3⇒変換3】を見つめる!(右図)
おっ!これはどちらの対角線も真ん中を通っている。(当たり前っかぁ!)
![]()
どうやら、真ん中に注目してやることがポイント?
![]()
けれども、「対角の3つの数字の和はどちらも15」というだけでは、何のとっかかりもつかめないよ!
![]()
では、【変換1】と【変換2】でも真ん中に注目してやるとどうだろうか?
![]()
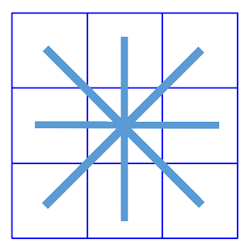
真ん中の数を含んでいる線は、縦線も横線もともに1本ずつあるよ!
これを、【変換3】と合成してやれば、全てのマスが網羅されることになりそうだ!(右図)
![]()
右図をしみじみと見つめる。
![]()
それぞれのマス目の数字はただ一つの直線にだけ属しているけれど、真ん中のマス目の数はナント4本の直線すべてに属している。
![]()
ということは、4本の直線分を全部足すと、真ん中の数だけが4回足されていて、その他は1回ずつ足されているという勘定になるぜ。
![]()
さらにさらに、ということは、9つの数字を全部足して、さらに真ん中の数だけ3個分足した数ということだ。
![]()
それぞれの直線はその直線上にある3つの数字の和で15と分かっていて、4本あるから全部を足せば60。
![]()
9つの数字を全部足した数は(1)でやってて、45だったから、60-45=15が真ん中の数の3個分だ。
よって、15÷3=5が真ん中の数ということになるぜ!
文章題を紐解けるための準備は、気持ちや方法論だけではできません。
結局は、最初はシミュレーションするしか方法はないものですが、それでも一つ一つの問題に「真剣な経験」として向き合うことと、それに伴う「失敗」が準備を完了させてくれることは確かです。
真打の文章題で真意を心に刻んでください!
最後に、これこそが文章題だと認めてもらえる例でまとめておきましょう。
【問題】
池のまわりに道があり、A地からB地までの道のりはどちらにまわっても等しくなっています。
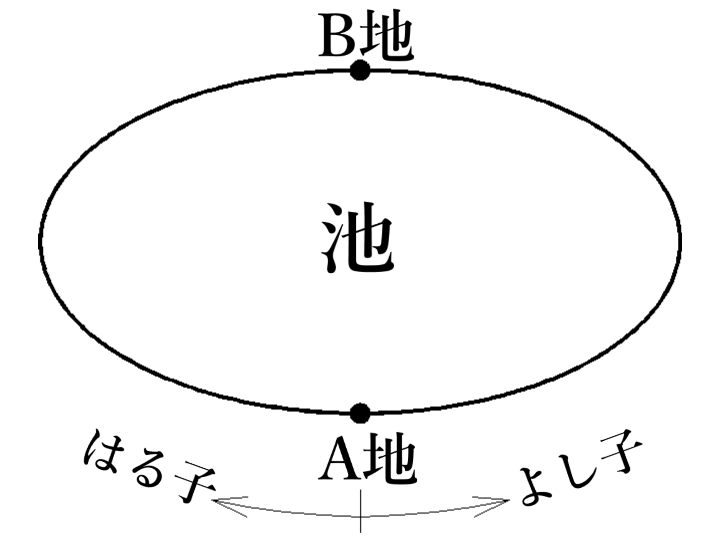
はる子さんは自転車で、よし子さんは歩いてそれぞれ一定の速さで矢印の方向にA地を同時に出発します。
はる子さんはB地を通過して12分後によし子さんに出会いました。
よし子さんはそれから20分後にB地を通過し、A地まであと2.8Kmのところで再び、はる子さんに出会いました。
- 1) はる子さんとよし子さんの速さの比を求めなさい。
- 2) はる子さんは自転車で1周するのに何分かかりますか。
- 3) よし子さんの歩く速さは毎時何Kmですか。
[神戸女学院中学 過去入試問題]
以下に記したことは、私の流儀では、あくまで最後に「こういうように考えることもできるよ」といったスタイルでフォローすることであって、実際の指導は、子どものペンの動きと顔を観察しながら、とにかく自分自身の力で答にたどり着くように、所用時間とタイミングを見計らってアドバイスで少し先を照らすことが最優先です。
子どもさんの考えや発想(有無にかかわらず)を起点にしないことには、子どもの成長などあり得ませんからね。
たとえ、算数以前に文章自体の意味が理解できていないにしても、与えられた図を使わせながら、逆に読解力以前の日本語の扱い方の基礎力を目覚めさせることもできると思いますよ。
子どもさんを観察していれば、そもそも日本語が理解できていないのか、それとも数学語に言い換えることができない段階なのかは、すぐに分かります。
これらのことをご理解の上、もし家庭塾で利用されるのであれば、決して塾の講義のように「こうだからこうでしょ!」「なぜ、こんなことが分からないのよ」的な指導で終わらないことをお願いいたします。
- A地からB地までの道のりはどちらにまわっても等しくなっています。
- はる子さんはB地を通過して12分後によし子さんに出会いました。
- よし子さんはそれから20分後にB地を通過し、
- A地まであと2.8Kmのところで再び、はる子さんに出会いました。
言いかえると、
「B地は1周の道のりのちょうど中間点」「B地は1周の道のりの半分\(=\frac{1}{2}\) 周の地点」
言いかえると、
はる子さんが道のりの半分を通過してから12分後に、
はる子さんの走った距離とよし子さんの歩いた距離の合計は池1周分の道のりになりました。
言いかえると、
よし子さんは、はる子さんが12分で走った道のりを20分で歩き、
言いかえると、
よし子さんが(1周の道のり-2.8Km)歩いた時間とはる子さんが(1周の道のり+2.8Km)走った時間は同じでした。
3.から、同じ道のりに要した時間が分かるのだから、速さの比は出てくるよね。小問 1)はこれでゲット!
一つ分かれば、ここからはいろいろな考え方ができますよね。
いくつか考えてみて、どれが一番カッコよかったかのコンテストを自分でやってごらん。それが一番勉強になることは保証してもいいですよ。
速さの比がでたところで、もう一度見直してみようか?
2.をさらに言いかえると、
はる子さんがB地を通過したとき(\(=\frac{1}{2}\) 周したとき)、よし子さんは\(\frac{1}{2}×\frac{3}{5}=\frac{3}{10}\) 周しているはずだから、出会うまでは\(\frac{1}{2}-\frac{3}{10}=\frac{1}{5}\) 周のへだたりがあったはず。
B地を通過してから、はる子さんは、よし子さんに出会うまでは、その\(\frac{1}{5}\) 周のうちの\(\frac{5}{8}\)、すなわちを\(\frac{1}{8}\) 周を走るはず。
ここは、【 8の隔たりがあれば、はる子さんが「5」、よし子さんが「3」を移動する 】と考えてから分数にしてやればいいのですよ。
無理やり最初から分数で答えさせようとすると「訳わかんない」子が多いもので、上のように考えさせていくと、自然に最初から分数で話すようになります。
さて、\(\frac{1}{8}\) 周を12分で走ったことになるから、1周を走る時間は\(12分×8=96分\)
小問3)は、「同じ時間に動いた道のりは、はる子さんを「5」とすれば、よし子さんは「3」だからその差は2」
4.から二人の動いた距離の差は2.8+2.8=5.6Km。
これが差の「2」に相当するから、「1」相当するのは2.8Kmと考えることができるね。
だから、はる子さんは、2.8×5=14Km、よし子さんは2.8×3=8.4Km
1周の道のりは、14-2.8=11.2Km(14Kmと8.4Kmのちょうど真ん中の値=平均)と出てくるね。
同じことだけれど、
「5」は「4」より1大きくて、「3」は「4」より1小さいから、「4」を池1周の道のりと考えると「1」が2.8Kmに相当すると考えることもできるよ。
この場合も、池1周の道のりは\(2.8×4=11.2Km\)と出てくるよね。
さて、ここまで来れば、はる子さんの走る速さが[道のり÷時間]で出てくるから、その速さの3/5ということでもいいし、先に、よし子さんが1周にかかる時間を出してから、[道のり÷時間]で計算してやってもいいよね。
\(96分=\frac{96}{60}時間=\frac{8}{5}時間\)
\(11.2÷\frac{8}{5}×\frac{3}{5}=11.2×\frac{3}{8}=4.2km\)
塾では「ダイヤグラム」を描けなどと教えられるかもしれませんし、それも間違ってはいませんが、きちんと一つ一つを日本語で理解さえすれば、たいがいは日本語だけで道筋は開けるものですし、算数は本来そういうものです。
たとえ、そうでないものでも、日本語できちっと算数語に言い換えるステップを経なければ、ゴールにたどり着くのは難しいでしょうね。
正式な資料ではないので、この程度の表現で終わっていますが、真意を理解していただければ幸いです。
むしろ、塾無しの家庭塾で子どもさんを指導されている方は、是非、参考にしてくださいませ。
おまけの文章題で算数語への翻訳にチャレンジ!
この問題はFAX塾において、当時5年生の教え子に配信した問題の1つです。
【問題】
学校のテストで、ある小数点どうしのかけ算の計算を間違えてしまいました。
「うっかりしたんだろうけど、小数点をつけ忘れていたぞ。本当の答えとの差は344.52もあったよ。」と言われました。
さらに、「元の問題は、先生もうっかりしてインクをこぼしてしまって一部しか見えないけれど、次のような式だった。元の式を復元して、正しい答えを求めて明日提出してください。」とありました。
言われた通り提出をしてください。
[ICL技術事務所過去生徒育成精選問題]
君たちの中には、文章題が苦手だという子もたくさん居ると思います。
あるいは文章題になると出来ないという子もたくさん居ますね。
この問題は、それほど長い文章ではありませんが、文章題で大切なことが詰まっています。
大切なことは、もちろん「まずは、文章の意味を理解することなのですが、
- 一つ一つの文章をおろそかにしないで、大切に噛みしめて意味を考えてください。
- 意味を考え、理解できた範囲で、その文章を算数語に翻訳してみることを覚えてください。
言葉にすれば、「言いかえると・・・」が口をついて出てくるようになればしめたものです。 - ただ、なかなか最初から思った翻訳ができるものではありませんよ。
「あぁ、そういう翻訳をしていたら、すぐに進む道が見えたんだ!」なんて思うことはしょっちゅうです。 - 大切なことは、その一つ一つの気づきを、その都度心に刻み込んでおいて頭の中の図書館に整理しておくことです。
- 問題集の答や指導者の解説を「フーン、なるほど」で終わっているだけでは、心に刻み込まれることはありません。
- 順序は、一旦全文を読み終えてからでもいいですし、一つづつ順番に翻訳しても構いません。
- マンガや図形や線図といったイメージで表すことになりますが、それを見て自分が分かればそれでいいのです。
- あるときは、箇条書きで書き出すことがベストなときもあります
- いきなり算数語に翻訳するのが難しいときは、「例えば、〇〇とすれば」ということで、簡単なこと小さな数で具体的に考えることを覚えておいてください。
- この後、イメージや算数語にしたことを、逆に普通の日本語で表現してやると、一挙に意味が理解できることもあります。
今、文章題に手も足も出ない君も、この作業を行うことで、文章題をこなせる準備が出来ていきます。
言い換えれば、この作業を続けている限り、いつかは文章題を受け入れ処理できるように必ずなりますが、意識的に頑張らないと、いつまで経っても何かを考える能力に劣ったまま大きくなるかもしれません。
数をこなすことばかりに焦って、自分が納得できないままにこういった作業を中途半端にしてしまうことが、成績としても悪い結果に繋がってしまうことを頭に入れておいてくださいね。
とは言っても、自分一人では何をどうしていいのかが分からない場合は、傍に誰かに付いてもらって、アドバイスをもらいながら自分で進める経験をすることが最も効果的です。
ただ、決して一から十までを教えてもらうことになっちゃうと、逆効果になりますから、そうはならないように注意してくださいね。
最近の家庭教師や個人指導の先生には、準備しないと指導ができない先生も多いようで、準備したことを自分から解説することに熱意があります。
高校生の場合はまだしも、小学生の場合には、一番やってはいけないことで、それこそ君の力を育てることとは程遠くなるんですよ。
だからこそ、私たちなんかは、小学生を指導することは大学受験生を指導することより難しいと思っていますよ。
この問題は、資料「数のセンスを鍛える17題」の最後の問題として収録していますので、下記の筋道に沿ってチャレンジしてみてください。
さて、この問題ならば、
- 小数点第2位でした → 〇.\(\triangle\square\)
- 小数点をつけ忘れた → 〇\(\triangle\square\) → これは、算数語ではどういうことになる?
- 本当の答えとの差 → 〇\(\triangle\square\)-〇.\(\triangle\square\)=344.52 → これは、算数語ではどういうことになる?
- 元の問題は??.175×1.???(?は何ケタかは不明)
といった作業を進めていきます。
分からない数は○でも\(\triangle\)でも記号を使って、〇.\(\triangle\square\) といったように当たり前のことでも書き始めることが大切です。
「そんなこと書いてどうにもならないよ!」なんて言ってると永久に「考える」こととは無縁の人になっちゃいますよ。
そして、算数語では「どういうことになるだろうか?」を考えてみてください。
そして、どうしても分からなければ、「ここまで書けたんだけど、アドバイスください。あくまでアドバイスだよ! 」って頼めばいいんです。









算数も数学も、本当は「謎解き」のように楽しいものだということ、知らせるべきが教師の務めと感じます。
杓子定規な授業の最初や合間に、その場限りで消えていくダジャレではなく、本質や種明かしを面白く披露してあげることができれば最高ですね。
それには自分自身が常に文献や専門雑誌を調べたり研究していかなければなりませんから、教師にこそ、そういう姿勢と環境を整えてあげることが必要だと思います。
学校の事務や親のクレーム処理や課外活動のサポートに追われているようでは、身心ヘトヘトでそれどころではなくなっちゃいます。