コロナウィルスによる非常事態宣言で、生徒さんも巣ごもり状態ではないでしょうか?
そのこともあって、ワープロ専用機データと紙ベースでしか残っていない過去の指導資料をWORDレベルで資料化する予定で推敲中の原稿を公開アップしました。
まぁ、こういった講義が受けられるのは一流講師が在籍する塾で、且つ、受講する権利を得た塾生だけであって、形態としては最も優れているはずの個人指導塾や家庭教師では、ほとんど受けることは出来ないと思います。
立方体とその展開図でセンスをつかむ
見取り図を描く
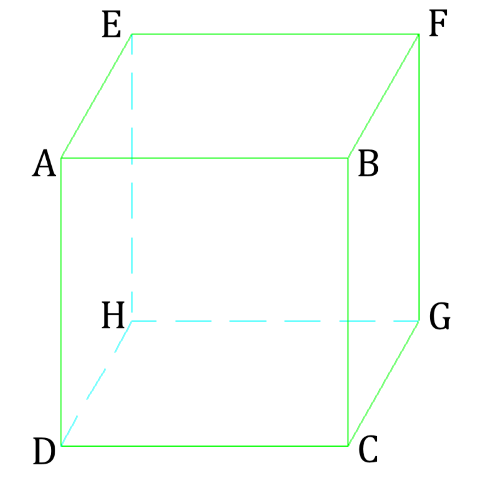

上の図を見ただけで、「あっ!立方体だ!」「あっ、正八面体だ!」って分かれば、それでいいよ。
頂点や辺についている記号は、今は考えなくても構いません。
正八面体は、中学生のために後半の資料としますが、中学入試でも出題されますので一緒に置いておきます。
自分で見取り図(立体図)を描けない君も、難しいことは考えずに、とりあえず上の図を描いてみて。
正確に描こうなんて思うと、コンピュータでも使わないと描けないんだから気楽にね。
見取り図なんて、現実の技術者の仕事でも、だいたいのイメージをつかむためだけのものだからね。
描き方はいろいろありますけれど、小学生や中学生で立体が苦手なら、バカの一つ覚えのように描き方を言われた通りに決めておけばいいと思いますから、後で説明しますね。
さて、まずは立方体の解体からいってみましょうか!
立方体は、別名「正六面体」
同じ大きさの正方形の6面で閉じられた立体ということは知っているよね。
さて、立方体の辺のいくつの辺をハサミで切ったら、展開図ができるかな?
見取り図を見ながら、どんな切り方でもいいから頭の中でハサミを入れて切ってみて。
どうしても頭の中で無理だったら、誰かに立方体を紙で組み立ててもらって、実際にカッターなどで切ってみればいいよ。
立体が苦手な君なら、まずはそこから始めることで間違いなく普通の立体感覚は身に着いてくるはず!
僕なんかも、どちらかと言えば立体感覚に優れているわけでもなく、数式の世界の方が断然好きですけれど、それでも機械の開発・設計ができているんだから、普通であれば十分という気持ちでいいんですよ!
3次元CAD(コンピュータ支援設計)が登場してから久しいですが、私たちのような自動機や産業機械の技術者にとっては2次元CADで十分に用をなしますし、無用の長物と感じる技術者が多いためでしょう、現実はなかなか3D-cadは普及しません。
私も3次元CADのデモンストレーションや講義を受けましたが、入り組んだ機構構成を持つ機械設計者には反ってウザイ以外の何物でもありませんでしたが、単純ではあるけれど曲面形状を持った金型や部品単体の設計などでは便利なのだろうなとは思っていました。
ただ、いつの日か主流にはなってくる可能性は高いと思うのですが、それでも私たちのようなメカニズムの世界では使い勝手が悪くて採用されないような気がしますし、たとえ業種にかかわらず普及したとしても、そのときは技術者も技能者も、より職にあぶれる事態になっているような気はします。
そして、何か所の辺を切ったら、展開図として机の上に広げられるかチャレンジしてみて。
そして、君の出した答えは、おそらく正解だと思うよ。
7か所(7つの辺)にハサミを入れて切り離せば、机の上に広げられる展開図になる!
君がハサミを入れたのと同じようにハサミを入れる人ばかりじゃないことは分かるね。
ハサミの入れ方によって、できた展開図は違うものになる。
むしろ、君のはさみの入れ方は少数派かもしれないよ。
ということになれば、立方体の展開図っていったい何種類できるんだろうか?
すぐには分からないよね!では、書き出して調べてみよう。
この作業のポイントは、
- 規則正しく書き出す
- 回転したり、表裏をひっくり返して同じになるものは数えない
ということなんです。
前者は、立体に関する特有の問題というよりも、どんな算数や数学に限らない、他のどんなことにも通じる【整理をするときのポイント】になるから、肝に銘じておいてよ!
結論
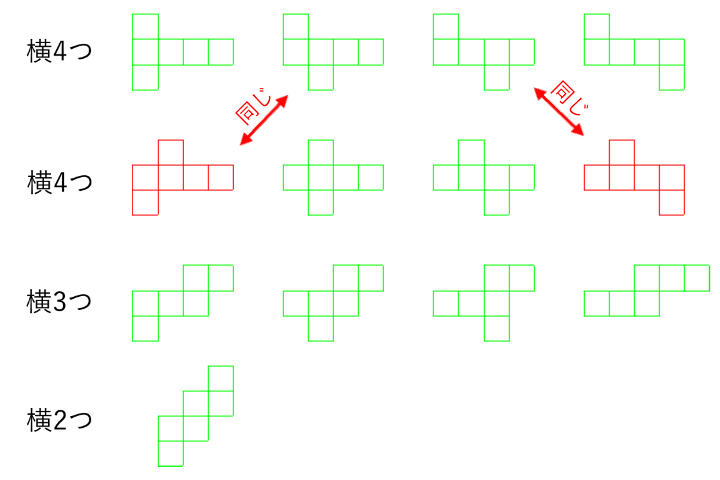
上の図の緑色の展開図がすべてです。
全部で11種類あります。
考え方
前提
横に5つ以上並ぶことはあり得ない。
何故なら、同じ並びでは立方体の面は4面しかないから、5つ並んでいると、二重に面を作ってしまうから。
1. 最大4だから、まず横に4つ並んでいるとして書き出します
A)残りの面は2つだから、まず4つ並びの上と下に1個ずつ配置する場合を考える。
- ①上側を左端に固定して、下側を配置すると4通りの配置の仕方がある。
- ②次は、上側を左端から2番目に固定して、下側を配置すると、やはり4通りの配置の仕方がある。
ここで、解説図のように①と同じものが出てきていることに気づかなければなりません。 - ③次は、上側を左端から3番目に固定することを考えますが、表裏ひっくり返すと左端から2番目ということになりますから、②でやった作業を繰り返すことになり、同じものしか出てこないことに気づかなければなりません。
B)残りの面の2つを上だけに配置する場合を考える。
下の図のような場合が書き出せるけれども、両端と、それぞれのお隣さんはひっくり返せば同じ。

さらに、下の図を見てください。

左端の展開図は折り曲げることはできますが、斜線の部分が同じところに来て重なってしまいます。
言いかえれば、6つの面のうち1つの面が作れませんから展開図としてはアウトです。
また、真ん中の3つ(実質上2つ)は折り曲げることができません。
それぞれの面が4つ密集してしまうと、折り曲げることすらできないことが分かりますね。
最後に、出来上がったすべての展開図で、4つの面が正方形に密集しているものはないことを確認しておいてくださいね。
したがって、B)の場合はあり得ないことになります。
2. 横に3つ並んでいる場合を想定して書き出します
A)残りの面は3つだから、まず3つ並びの上と下に2個と1個ずつ配置する場合を考える。
1)の結果を考えて明らかになった「それぞれの面が正方形として4つ密集することはあり得ない」ことは分かったから、ここでは、可能性としても、もう書き出すことはしないよ。
さらに、上と下に1個ずつと2個を配置する場合は、ひっくり返せば同じものになると考えられるけれど、とりあえずやってみて確認だけはしておく方がいいよ。
B)残りの面は3つだから、3つ並びの上だけに3個を配置する場合を考える。
これが、なんと!結果の図のようにあり得るんだよね。
3. 横に2つ並んでいる場合を想定して書き出します
A)残りの面は4つだから、2つ並びの上と下に配置する方法は、
- 上に4つ(下に4つもひっくり返せば同じこと)
・・・4つ並びは1)で考え済みなので必要無し! - 上に3つ、下に1つ(上に1つ、下に3つもひっくり返せば同じこと)
・・・3)で考え済みだから必要なし - 上に2つ、下に2つ
・・・これは、まだ考えたケースにはないから、考えるべし!
これらの、方針に基づいて書き出した結果が11種類だというわけです。
「洩れなく、無駄なく、美しく」とは、こういうプロセスのことを言うんです~。
さて、書き出した展開図をながめてみて、何か気が付くことはあるかな?
実は、2つのことが分かっちゃう!
- 展開図の周の長さは、どれも同じだ!そして、辺の数にすれば14辺分だ!
- 展開図でつながっている箇所の数は、どれも5か所だ!
何故、そんな一致点があるのでしょうね?
それには、次のようなわけがあります。
立方体は正方形が6面でできていましたね。
言いかえると、6つの同じ正方形をパーツとして、立方体は出来ているというわけです。
そこで、6つの正方形パーツを個別に下の図のように並べてみましょう。
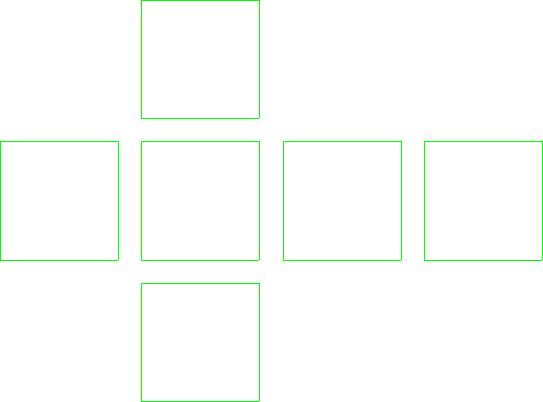
辺の数は、全部を合わせると、4×6=24個あります。
ここから、例えば下の図のように、2つの正方形をくっつけてみましょう。
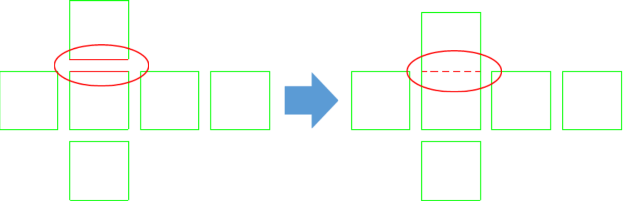
どうなりましたか?
2つの辺はくっついて1つの辺に統合されましたが、もはや、周の長さには参加しなくなっています。
このくっついて1つになった辺を折り目として点線で示しておきましょう。
ばらばらの正方形パーツとしては24個見えていた辺が、2つのパーツをくっつけることによって、周の長さには参加しなくなったのですから、この段階で、周の長さは2だけ減って、24-2=22辺分となっています。
さて、残っているパーツでくっつけられる箇所は何か所ありますか?
あと4か所残っていますね。
同じように順番にくっつけていくと、周の長さは2辺分だけ4回減ってきますよね。
ですから、22-8=14辺分が、くっつけ終わったときの周の長さになります。
最初のパーツのくっつけからまとめておくと、
- ばらばらの正方形パーツの辺の数は、4×6=24辺
- 2つのパーツをくっつけると、周の長さに参加している辺が2つ減る。
- くっつけられる箇所は5か所ある。
- 5か所をくっつけると、周の長さに参加している辺は2×5=10個減る。
- くっつけ終わった段階で、パーツの辺のうち、24-10=14個の辺が周の長さに参加している。
このことが、すべての展開図にあてはまるかどうかを確認してみてください。
少し分かってきましたね。
ばらばらの6つの正方形パーツから、5か所の辺どうしをくっつけると、立方体の展開図ができた!
(下図)
折り目に沿って折り込んでいくと、立方体ができ上る様子を頭の中でイメージできるかな?
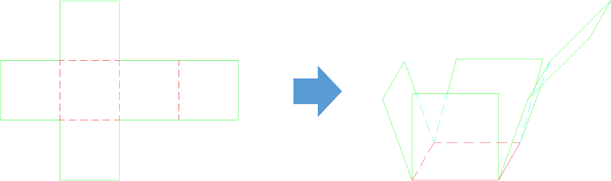
さて、展開図を折り曲げて立方体にしていく様子を表した右図を見ていくと、周の長さに参加していた辺のどれかとどれかがピタッと一致していくことが分かるよね。
すなわち、展開図で周の長さに参加していた14個の辺は、立方体に組み立てるときにピタッと一致するペアが7組あると考えることができる。
逆に言えば、立方体の状態からハサミを入れて切り離したペアが7組あるということになる。
あるいは、立方体は7か所の辺をハサミで切り離せば、展開図にできるということなんだね。
分かるかな?
ここで、予告編として正八面体の場合の種明かしをしておくと、
- ばらばらの正三角形のパーツ8つの辺の数は、全部を合わせると3×8=24個あります。
- 立方体の場合と同じなんですよ。
- そのパーツから7か所の辺どうしをくっつけると、正八面体の展開図ができるんです!
- そして、正八面体の12個ある辺のうち、5か所の辺にハサミを入れて切り取ると展開図にできるんです。
展開図としては、つながっている辺と切り離す辺の数が、5と7か7と5かの違いになるんですね、
「何故か?」なんてことまで考える必要はありません。
正方形が6個集まってできる立方体と正三角形が8つ集まってできる正八面体は兄弟分とぐらい意識していればそれでいいですよ。
展開図を組み立てて立方体を作るとき、どの辺とどの辺がくっつく?
くっつく辺どうしに同じ記号をつけて確かめてみよう。
ここが立体感覚をつかむためのスタート点だから、絶対にサボらないでよ!
この作業をしておかないと、「立体感覚」なぞは一生身に着かないままで終わるよ。
下記の解説用図は記号と色と両方で分けてありますが、まずは自分で辺と辺の対応を書き出してみてください。
対応させるには、頭の中で展開図を折り目に沿って折り曲げていく様子を思い描かなければなりません。
それを、何とか出来るようにしようとするチャレンジの中にしか「立体感覚」は育っていきませんよ。

続きは、キリのいいところまでの草稿ができ次第アップして参ります。








