二次式・二次方程式・二次関数の関係性理解が数学の基幹です
一般的にもそうなのですが、お受けする質問からもやはり、二次式、二次方程式、二次関数がバラバラの知識でしか理解できていない子が多いように見受けられます。
この基本だけでも入試の半分を占めると言っても過言でないほど高校数学の幹となっている最上流の概念ですから、夏休みの際に完膚なきまで体系化しておきましょう。
その他の単元をやる時も常につきまとってくる最上流概念ですから、ここをあやふやにしておくと本当に数学が伸びることなどはあり得ないこととなってしまいます。
逆に、ここを体系化して突破してしまうと、数学とはこんなに簡単なことしか言っていなかったのだと気付くことでしょう。
実は、資料は徹底的にこの体系化を意図して書かれていますので、重複する部分が多々出ますが、質問への回答とした資料を使いながら、超初心者レベルでステップ・バイ・ステップにまとめていきます。
とは言っても、数学を暗記や操作で乗り切っている、そこそこ成績優秀者の中にも、知識がバラバラな諸君も多々おられます。
バカにせずに一読の上、体系的に理解すれば、もっと楽に成績を伸ばせますよ。
この夏期特別レポートで、公式を丸暗記していた自分を、「なんとムダな時間を浪費していたのだろうか!」と恥ずかしく思うかもしれません。
それでは、理解するためのケーススタディ素材として、【\(x\) に関する二次式 \(x^2+x-2\) 】を対象としてスタートしていきます。
【言葉の使い方】
※下記は、それぞれの言葉の定義ではありません。
あくまでも、\(x^2+x-2\) を対象として言葉の違いと関係性を理解してもらうための例です。
① \(x\) に関する二次式とは、⇒ \(x^2+x-2\) そのもののこと。
② \(x\) に関する二次方程式とは、⇒ \(x^2+x-2=0\) のこと。
「\(x\) に関する二次式が0になる特殊な場合を考えるよ」ということ。
③ \(x\) に関する二次関数とは、\(y=x^2+x-2\) のこと。
「変数\(x\) によって値が変わる式の値を変数\(y\) と置いてやるよ」ということ。
二次式、二次方程式、二次関数の言葉の違いを、上の感覚でまず理解しておいてください。
ここで、いちいち「\(x\) に関する・・・」と書いているのは、単なる「二次式」とだけ書かれた場合は、例えば、\(x^2+xy-2\) などのように多変数の二次式も含まれるからです。
それで、1変数 \(x\) だけで式が構成されている数式に限定したい場合には、厳密には「\(x\) に関する」という修飾語をつけなければならないということなんです。
一般的に「二次関数」と言えば、「\(x\) に関する二次関数」が指されるわけなんですが、例えば、\(f(x,y)=x^2+2xy+2y^2-3x+4y+5\) も「二次関数」であるということは頭に入れておいてください。
この場合は、厳密に言うと「\(x\) 、\(y\) に関する二次関数」となり、数Ⅱや数Ⅲではよく出てきます。
即ち、単に「二次関数」と言う場合、本来は放物線だけを表すのではないのですが、文脈上、あるいは通念的に、「\(x\) に関する二次関数」=「グラフが放物線になる関数」が指されることが多いという程度の認識はしておいて欲しいのです。
それでは、本特別講座の内容を体系化マップで次に示しておきます。
それぞれの項目はしっかりと理解している、暗記している諸君は、このマップを眺め確認するだけで、第2の壁を破ることができることでしょう。
二次式・二次方程式・二次関数の関係性理解マップ
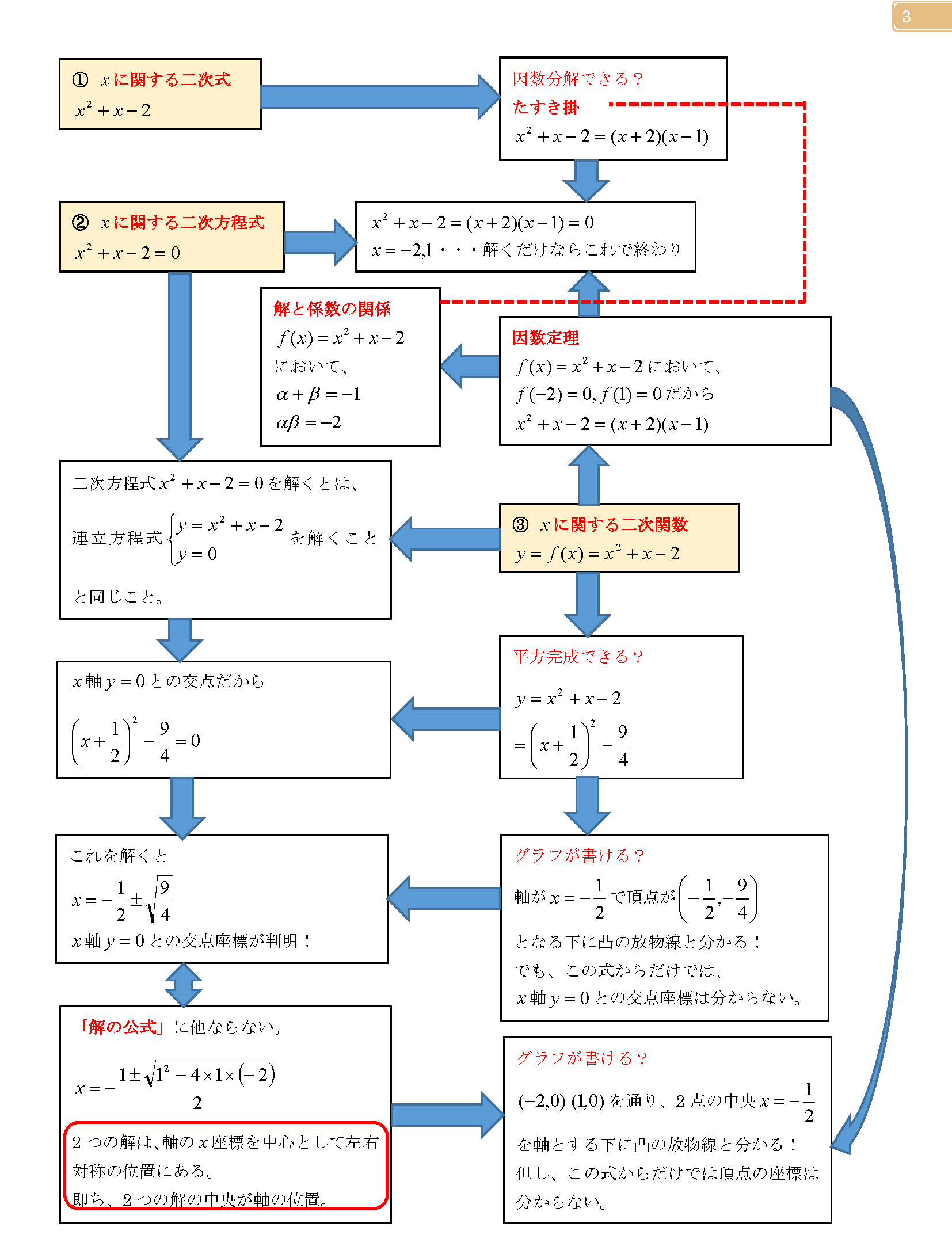
二次式・二次方程式・二次関数を体系的に理解する講座
下記よりPDFファイルとしてダウンロードできます
尚、本夏期講座内容は、資料『帝都大学への数学 vol.3:知っ得で知っ解く二次関数(放物線)』のイントロ部分になっています。
この超初級講座をクリアされたら、引き続き、資料で底上げを図ってくださいね。
さすれば、上記ページでご披露している資料の仕上げ問題(平均的な生徒が少し背伸びをすれば届くレベルであり、取りこぼさなければ難関大学にも合格できるレベル)も、ほぼ解けるぐらいにはなっている筈ですよ。
「この夏休みには二次関数を制覇するぞ!」
そういうテーマ・課題を持って、計画的にコツコツと遂行することこそが重要です。
夏休みだけではなく普段から、このような姿勢で自分の勉強時間を決まって確保している生徒は必ず合格します。(種明かしの1つです)
テーマも計画性もなく、行き当たりばったりで日々の課題をこなしているだけでは、同じ時間を勉強していても、間違いなく結局は身に着かない無駄な時間に帰します。(合格する生徒と合格できない生徒の決定的で特徴的な差)
次の「二次式・二次方程式・二次関数」は、たすき掛けができないって!因数分解に躓く生徒が知っておくべきその正体(夏期講座超初級2)









目から鱗です。
現在の中学では関数を1年2年3年でバラバラに分けて学習しなくてはなりませんよね。なので、関連性がわかりにくいと感じています。
このサイトを、私の生徒たちにも見てほしいです。