二次式で絶対値を学び直す!助け合うグラフ脳と式脳を作れ!
さて、ついでに二次関数を通して「絶対値」という概念を復習しておきましょうか!
本講座の素材にしている二次関数では、\(y=|x^2+x-2|\) ということになります。
絶対値に関しては、【帝都大学へのビジョン】の本編に、例えばとしての説明として挿入していたのですが、何と翌年の慶應大学経済の入試にそのままみたいな問題が出題されたと報告を受けてびっくりしたエピソードがあります。
こちらは、絶対値の概念を日本語で理解していれば、必要以上に難しく考える必要はないという意図で書き記したものですので、機会があれば読み直してください。
絶対値とは、0からのへだたりのことであるからマイナスはありません。
-4の絶対値は4ということです。
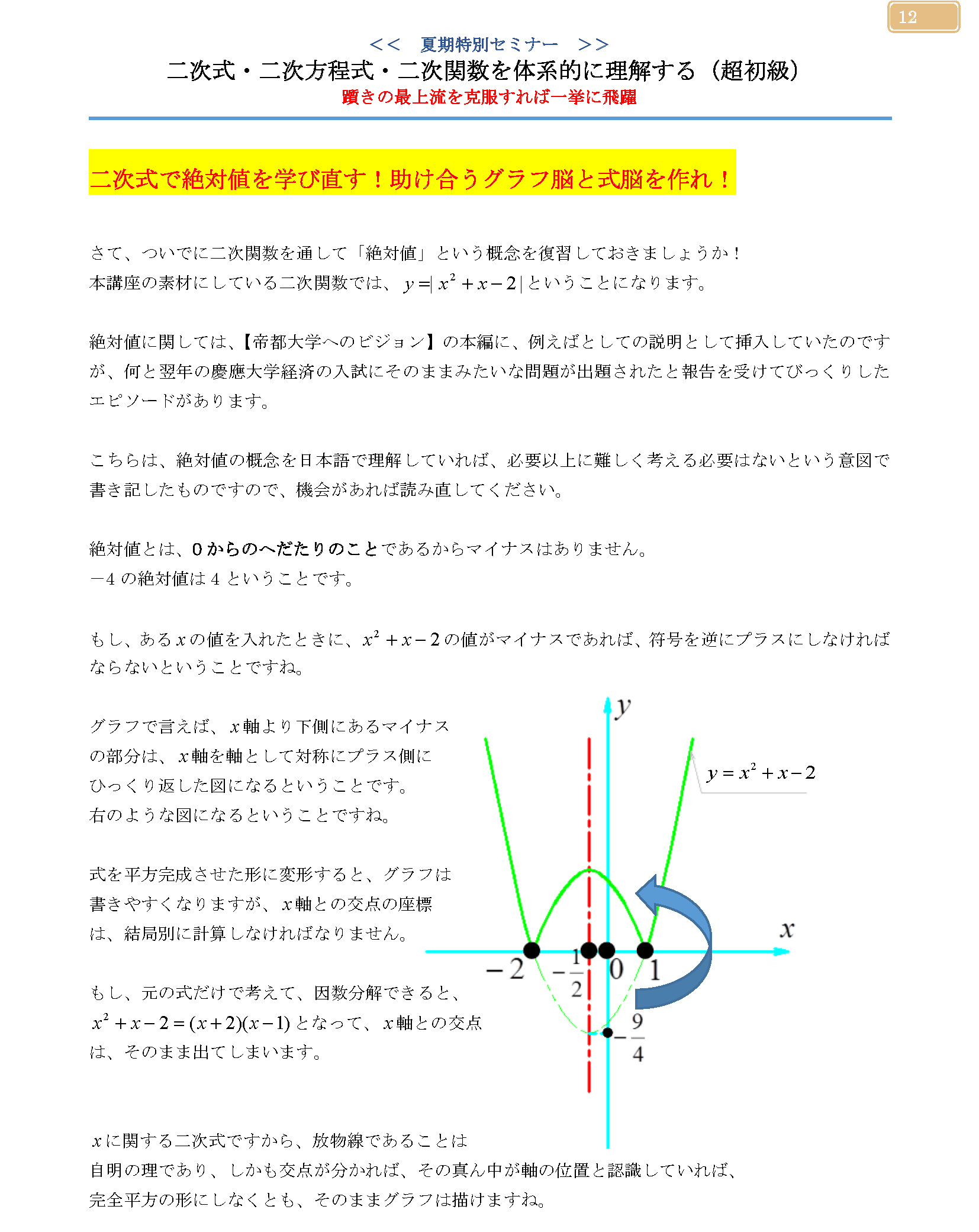
もし、ある\(x\) の値を入れたときに、\(y=x^2+x-2\) の値がマイナスであれば、符号を逆にプラスにしなければならないということですね。
二次式で学び直す絶対値!
二次式・二次方程式・二次関数を体系的に理解する講座
下記よりPDFファイルとしてダウンロードできます
尚、本夏期講座内容は、資料『帝都大学への数学 vol.3:知っ得で知っ解く二次関数(放物線)』のイントロ部分になっています。
この超初級講座をクリアされたら、引き続き、資料で底上げを図ってくださいね。
さすれば、上記ページでご披露している資料の仕上げ問題(平均的な生徒が少し背伸びをすれば届くレベルであり、取りこぼさなければ難関大学にも合格できるレベル)も、ほぼ解けるぐらいにはなっている筈ですよ。
「この夏休みには二次関数を制覇するぞ!」
そういうテーマ・課題を持って、計画的にコツコツと遂行することこそが重要です。
夏休みだけではなく普段から、このような姿勢で自分の勉強時間を決まって確保している生徒は必ず合格します。(種明かしの1つです)
テーマも計画性もなく、行き当たりばったりで日々の課題をこなしているだけでは、同じ時間を勉強していても、間違いなく結局は身に着かない無駄な時間に帰します。(合格する生徒と合格できない生徒の決定的で特徴的な差)
前の「二次式・二次方程式・二次関数」は、二次方程式「解の公式」覚えていないって!数学は暗記じゃないことの典型(夏期講座超初級3)








