正多角形と方程式 \(x^n-1=0\) の不思議な関係

正三角形と方程式 \(x^3-1=0\)、正方形と方程式 \(x^4-1=0\)

複素平面（ガウス平面）に、実数の1を起点として、単位円上に正三角形と正四角形（正方形）を書きます。

「それがなんなん？」と思うかもしれませんが、実際に描きながら、この図が何を表しているのか、しばし眺めて考えてみましょう。

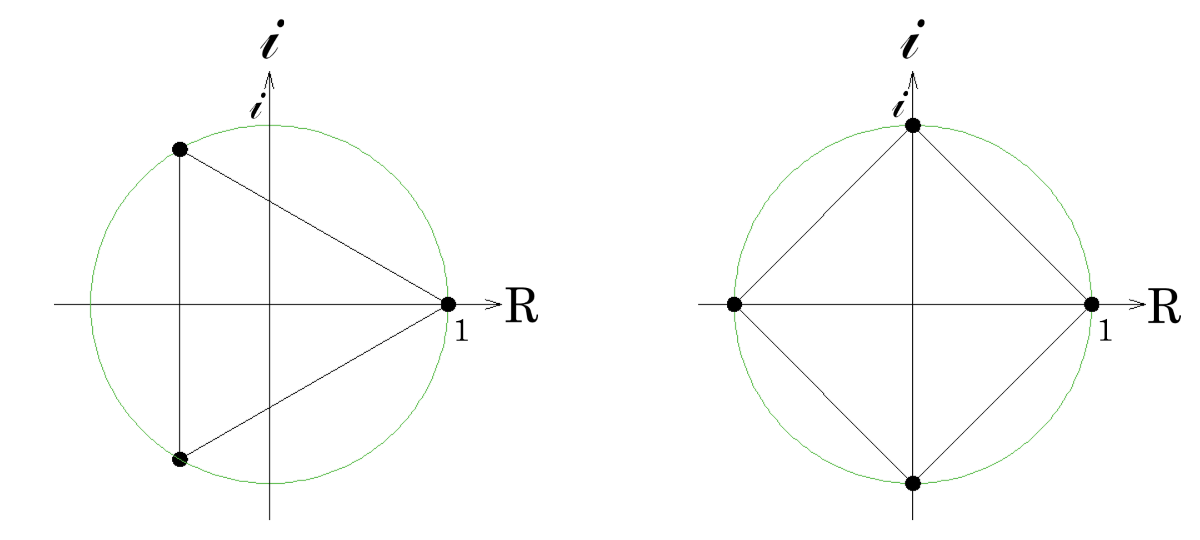
実は、それぞれの頂点は、それぞれの方程式 \(x^3-1=0\)、\(x^4-1=0\) の解を表しています。

「解」と言っても、学校で要求されるのは実数解だけですから、前者は\(1\)だけ、後者は\(1\)と\(-1\)の2つの実数解があることになります。

君が高校生なら、この程度の方程式は因数分解によって答えを出せるはずですよね。

さて、君も「n次の方程式にはn個の解がある」という話しは聞いたことがあろうかと思うのですがどうでしょうか？

これは、「複素数の範囲での解」ということであり、実数よりも範囲を拡げた数の世界でのお話になります。

この図で言えば、実数というのは横軸（図ではRealの意味でR軸）の上にしか存在しないのですが、その上下には虚数（\(i\)）を含んだ広大な世界が宇宙のように拡がっています。

大変な人気記事となってしまった「複素数が暴く直角整数三角形」で使った「素数を分裂させる」などという曲芸ができるのも、この複素数の宇宙のお陰です。

複素数が暴く直角整数三角形

ではここで、描いた正三角形と正方形の頂点の実数部分と虚数部分の数値を出してみましょう。

正方形の方は何もすることがありませんが、正三角形の方は少し計算をしなければなりませんね。

とは言っても、30°、60°、90°の直角三角形（正三角形を2等分した直角三角形）の短辺の長さは斜辺の半分という小学生の知識と中学生の知識ピタゴラスの定理さえ知っていれば出ますね。

高校生の君は、それぞれ因数分解して、\(x^3-1=0\) の場合は「解の公式」から複素数範囲での解も出してみて下さい。

そして、それぞれ、上で幾何的に求めた正三角形と正方形の頂点に対応する複素数と一致することを確かめてみましょう。

正五角形と方程式 \(x^5-1=0\)、正六角形と方程式 \(x^6-1=0\)

上の例が何だか不思議だと思ったら、正五角形、正六角形と確かめてみたくなりませんか？

次のような図を描くことになります。

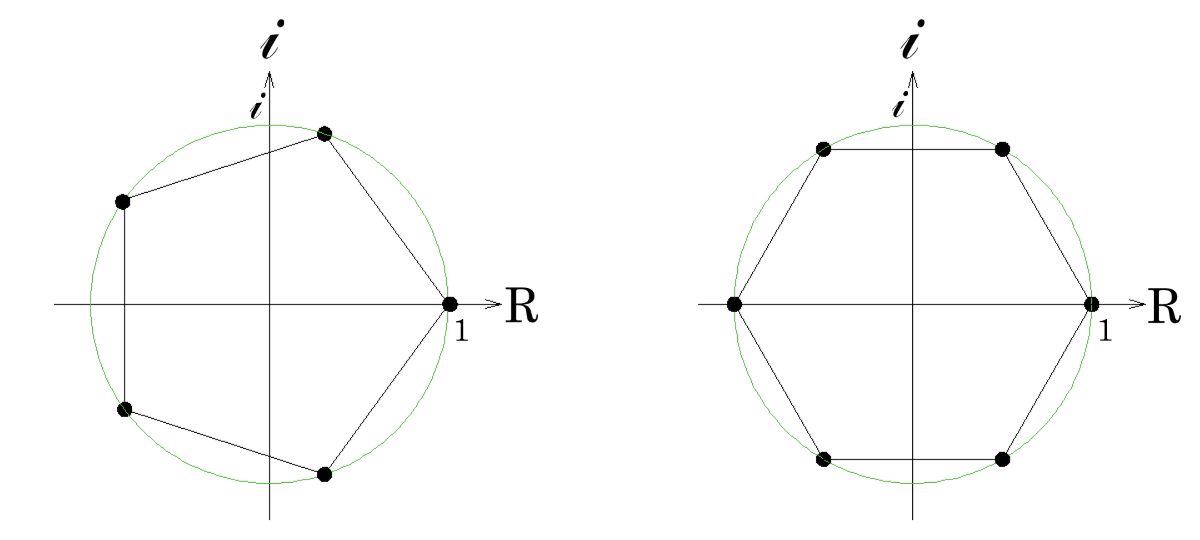
結果は最後に示しますが、正五角形の方がややこしそうですね。

正六角形は正三角形と同じく60°絡みだから計算しやすいね。
正五角形は72°絡みだから小学生の知識では計算できないけれど、三角関数に関する基本公式を駆使すれば18°、36°のsinやcosは計算で求められるのね。
ヒントは「\(36×5＝180\)」
幾何としても相似を利用すれば、ピタちゃんの定理と合わせて値が出ます。（図の中でも補助線を引けば浮かび上がる二等辺三角形ですが、浮かび上がっても着眼することが難しいかもしれませんし、着眼できても、\(\sqrt{ }\)を習っていない小学生には無理です）
必ず、因数分解によってもすべての解を出せるようにしておきましょう。
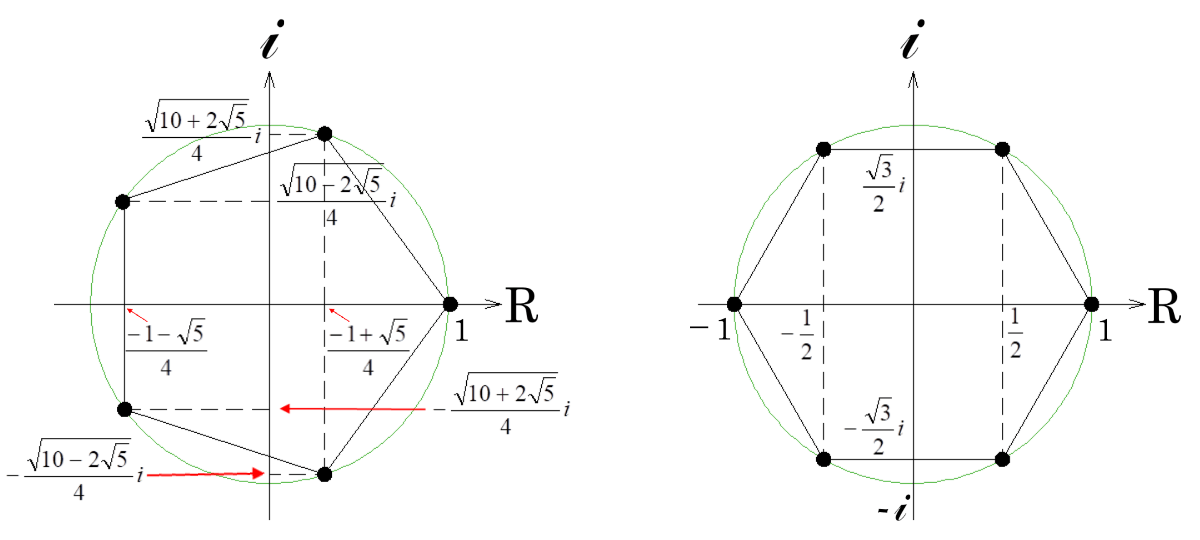
資料「因数の頭に解宿る」を読まれた会員様なら、簡単にできるはずです。
これを見ると、偶数乗時は\(1\)と\(-1\)の2つの実数解があるけれども、奇数乗時は\(1\)のみしか実数解は存在しないことが分かりますね。
これは因数分解を規則性から眺めると「なるほど」とうなづける対応になっています。
ちなみに正五角形の辺の長さと対角線の長さの比は、\(\tau＝\frac{1+\sqrt{5}}{2}\) と黄金比になっています。
資料「フィボナる・リュカる」にも記した「黄金比」と対照して楽しんでください。入試問題での昨今の潮流「確率の漸化式」の攻略にも役立ちます。