複素数が暴く直角整数三角形～虚数もこんな風に教えられたら・・

整数直角三角形と複素数の不思議な関係

君は、

あるいは、

を知っているのではないでしょうか？

今日は、そんな直角三角形とは全く無縁そうで、誰も連想すらしないであろう複素数が、直角整数三角形を暴いてくれるというお話のさわりに関するイントロだけをご紹介しておきたいと思います。

誰にでも分かりやすく全部書いちゃうと、教育業者の誰かや小遣い稼ぎのライターに勝手に使われちゃう時代だから、イントロだけに留めておきます。

それでも、これを読んでいただいただけで、「虚数や複素数をこういうビューからも説明してもらったら、私も数学が好きになれたかも」と感じてもらえる方もおられるかもしれません。

さて、直角を挟む2辺の長さが整数である直角三角形は無数にありますが、その中で斜辺も整数になる三角形の長さのセットを(3,4,5)以外で問われたら、なかなか思い浮かばないのではないでしょうか？

斜辺の長さで正解を挙げていきますと、5,13,17,25,29,37,41,53,・・・となります。
この8つの整数から、共通するものはないでしょうか？

ここまでは、小学生の君にでも気が付いてほしいところなのです…。

さて、「素数」と言いたいところですが、25が入っていますから正解とはなりません。
他に、すべてに成立する共通点があります。
「刑事の勘」ならぬ「野生の勘」を働かせて見つけてみて下さい。

そこで、これらの数の中から素数だけ（25などの素数でないものを除外）ピックアップすると、素数ですから素因数分解はできませんが、複素数の概念を導入すれば、分裂させることができるという共通点があります。

そして、その分裂を起点にすれば、次々と整数直角三角形が作れます。

例えば、斜辺の長さが5である直角整数三角形を例にとると、斜辺の長さ5には、
\((2+i)(2-i)=4-i^2=5\)
というシンプルな分裂式に持ち込めます。

これが、『素数の分裂』なのです！！

そして、分裂の片割れ\((2+i)\)を2乗すると、
\((2+i)^2=4+4i+i^2=3+4i\)
斜辺を5とする直角三角形の残り2辺の長さ3,4が現れます！！

もう一方の分裂の片割れ\((2-i)\)を2乗しても、符号は変わりますが、3,4が現れることに変わりはありません。

5を素数分裂させたら\((2+i)(2-i)\) → その片割れを2乗したら3と4が \((3±4i)\) という形で現れた！

続いて、その\((3+4i)\)を2乗してみましょうか！？
\((3+4i)^2=9+24i+16i^2=-7+24i\)

前式の経緯を考えますと、直角を挟む2辺の長さが7と24の直角三角形が連想されますね。
実際に、この直角三角形の斜辺の長さはどうでしょうか？

結果は25です。
そして、25を素数分裂させたら5×5であると同時に　\((3+4i)(3-4i)\) ・・・、不思議ですね！

興味が湧けば、\((3+4i)\)を続いて、3乗,4乗,・・と検証してみてください。
何だか面白い結果が出てきますよね。

さらに、例えば、斜辺の長さが13である直角整数三角形を想定して、同じように13を分裂させてみてはどうでしょうか？
そして、同じように考えていけば、すべての辺の長さが出てきたのではないですか？
高校2年生ならできるはずなのですが…。

嫌われ者の虚数も、どうやら途方もなく世界に広がりを持たせてくれている陰の立役者であることの一番シンプルな例でしょうか！

この後の続きは、会員限定での資料とする予定です。
お楽しみにお待ちください。
いやいや、あなたが資料化してくださってもいいのですよ！

いやいや、むしろあなたが、この解説をチラシの裏にでも書いて、じっくり「ホンマかいな？」となぞり書きして、ここから先を考えようとしてくれることを期待して書いています。
もし、そんなあなたが沢山現れたら、日本もまだまだ安泰でいられるかもしれませんから…。

「チラシの裏に書けって言われても、何を書くんだよ～？」って君には、次のヒントを与えておきましょう。

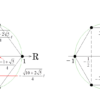
複素平面（ガウス平面）に\((2+i)\) の点を打って、原点と直線で結んでおきます。
ある複素数に\(+i\) を掛けるということは＋90°回転ワープすることであり、\(-i\) を掛けるということは-90°回転ワープすることだと考えてください。
共役同士の掛け算、\((2+i)(2-i)\)は、 \((2+i)\) を単に2倍したものと、\(-i\)倍したものを足し合わせたものです。
同じ複素数同士の掛け算、\((2+i)(2+i)\)は、 \((2+i)\) を単に2倍したものと、\(i\)倍したものを足し合わせたものです。
掛け算や足し算は、普通の座標系やベクトル系と同じように考えることができます。

これを、チラシの裏に書いてみれば、この原理が実に当たり前のことであることが分かります。

そして、君が思いつく数のペア\((a+bi)\)に、この原理を適用すれば、その度に整数直角三角形が出来ちゃうことを体験することができます。

原理が分かれば、次は整数直角三角形が成立しうる辺の長さのルールを数字と日本語で説明できることになります。