Yahoo知恵袋で下記のような質問がありましたので初めて回答しちゃいました。(笑)
それにしても、次から次へと質問があるのは分かりますが、投稿されて30分ほどなのに回答がどんどん入って来てるみたいで驚きました。
あれって、質問を待ち受けているんでしょうかね?
それと、ネットでも塾を中心として「和差算」の説明が沢山出ていますが、分かりやすいとか分かりにくいとかの前に、すごく機械的な解説が多いんだなぁと感じました。
小3の算数です
答え
①200
②100
③20
④10
⑤8足して800になる式を引き算して①?⑤の答えを出すと言うのはどう言う風に考えれば良いのか教えてください
②の答えの例)
450+350=800
450-350=100
■回答
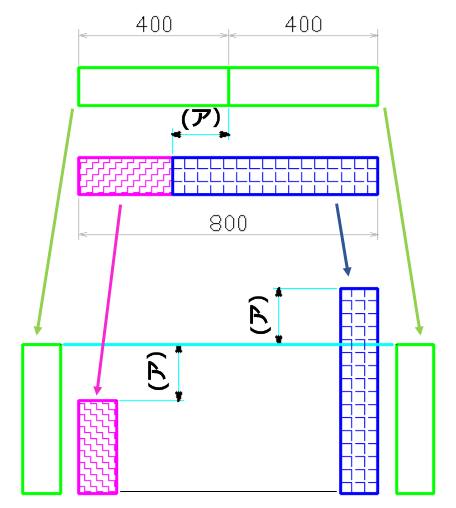
長さが800mmある長い羊羹が2本あります。
その内の1本(緑)を今、ちょうど半分で切ったまま分離せずに置いておきます。
もう1本の同じ羊羹をその下に、左右同じ位置に並べ、
1本目のちょうど半分の切り目から(ア)mmだけ左側で切ります。
左側の短い方(桃)と右側の長い方(青)に切れました。
その後、それぞれの羊羹を下面を一直線上に合わせて左右に立てて置きます。
同じ長さに切った緑の羊羹は上面も同じ水平線上で一致します。
長さに差は無いということですね。
一方、短い桃色の羊羹は緑の羊羹より(ア)mm短く、長い青色の羊羹は緑の羊羹より(ア)mm長いですね。
そうすると、その長さの差は(ア)mmの2倍あることになります。
(ア)mmが10mmであろうが20mmであろうが、この結論に変わりはありません。
2つの羊羹の足した長さが同じである限り、その2つの羊羹の長さは、ちょうど半分の羊羹の長さとの差分は同じなのですが、片や短くなり、片や長くなるだけのことなのです。
即ち、2つの羊羹の長さの差は、
・長い方の羊羹の長さとちょうど半分の長さの羊羹の長さとの差の2倍
・短い方の羊羹の長さとちょうど半分の長さの羊羹の長さとの差の2倍
いずれとも表現できるわけです。
となると、
①差が200mm → 片や半分より100(200の半分)短く、片や半分より100(200の半分)長い
よって、400-100=300と400+100=500になります。
②差が100mm → 片や半分より50(100の半分)短く、片や半分より50(100の半分)長い
よって、400-50=350と400+50=450になります。
③差が20mm → 片や半分より10(20の半分)短く、片や半分より10(20の半分)長い
よって、400-10=390と400+10=410になります。
以下、同様ですね!!
これを、巷では【差分算】と呼んでいるようです。
これを、乗客が乗るカゴの反対側も錘ではなくカゴであるような風変わりなエレベータ(実際には不便でたまらん!)で説明しても子どもは喜びますよ。
少し難しい物言いをすれば、
合計が等しいような2つの数は、ちょうど半分の数を基準にした時に、一方の数を基準より少なくした場合、もう一方の数をその分基準より多くしなければならず、2つの数の差は、「その分」+「その分」、すなわち、「その分」の2倍になるということですね。
式で表せば、
- (A-ア)と(A+ア)は足せば、いつだって2Aになるよ
- 足せば2Aになるような2つの数は、いつでも(A-ア)と(A+ア)のペアを組んでるよ
ということですね。
でも、これだけ説明すると、「奇数の時はどうするねん?」と食ってかかる方が居られます。
小学生なら、「こいつ、良い質問するな!」なんですけれどね…。
例えば、合計が799なら片方は399を基準にして、もう片方は400を基準にすればいいだけの話で、そもそもの基準どうし最初から1の差があるだけです。
偶数の時は、基準が同じ数(2つの数の差が0)に取れるというだけなんですね。
- (399-ア)と(400+ア)は足せば、いつだって799になるよ
- 足せば799になるような2つの数は、いつでも(399-ア)と(400+ア)のペアを組んでるよ
この問題の800を799に変えて、問題を解いてみてください。
この時、2つの数の差を変えてやらないと問題が解けないことがお分かりいただけると思います。
それでは、最後に『差分算のエレベータ』をPDFファイル2枚でご紹介しておきましょう。
子どもたちは面白がって、結構好評だった説明です。
そして、流水算も理屈は同じだということやマイナスの数を引くことを理解するきっかけに出来るかもしれません。
あまり、「和差算」だとか「差分算」だとかの言葉にとらわれずに、素直に理屈を絵にして考えるクセをつけることが大切です。






