塾へ行くのが嫌で通塾していなかったのに、いつも成績はクラスでトップの子を指導した際の残存資料より、下記の『場合の数』5題を通して、そのポイントやコツを掴んでいただければと思います。
そんな彼も、結局は、FAX方式にプラスして当方の事務所まで来ちゃうようになってしまいましたので、結果的に「通塾」になってしまいましたが…。(笑)
彼のために執筆したのが、【数学脳への導火線 05-丸竹夷二押御池~場合の数とは?】。
「丸竹夷二押御池」は京都の通りを覚えるためのわらべ歌のフレーズなんですが、それを『ヨ・タ・ヨ・タ』方式で歩くことで「場合の数」を指導したら、メッチャ受けました。
ALLコースの方、中学受験&保護者コースの方のみ資料室でしか見れないので申し訳ないのですが…。
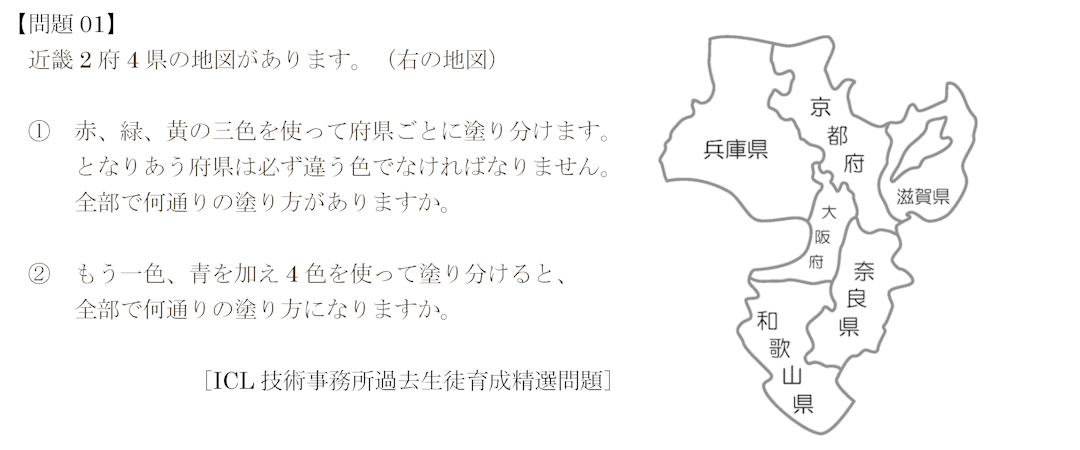
君たちの中には、『4色問題』という名前を聞いたことがある子もおられるかもしれませんね。
昔から有名な問題だったのですが、コンピュータ技術の目覚ましい発展によって、初めて解けたというほどの難問題だったんですね。
ちなみに、僕は、75年頃に電気工学科まで越境して『グラフ理論』の講義を受けたんですが、その時の教科書には「いまだに証明が与えられていない」となっていたんですよ。
この問題をすごく砕けた言い方で説明しておくと、
【例えば、世界地図において国境を明らかにするために、各国を色分けするとすれば4色で足りるだろうか?】
という問題なんですね。
国境を明らかにするための条件を含む条件は次のように定められます。
- 隣り合う国は違う色を塗らなければならない
- 但し、点だけで接する2つ以上の国は同じ色でも構わない
- 海も一つの独立した国として色を塗る
なんだか、「そんなに難しいの?」と思ってしまうかもしれませんが、問題は「どんな地図であっても4色で足りるか?」ということを証明しなければならないところが難しいのですね。
『算数』とは違って『数学』になるわけです。
見ての通り、ここに出題した(1)の問題は、まず『3色問題』、そして『4色問題』を極めて小さい範囲で具体的に考えてみよう版の『算数』なんですね。
我ながら、なかなか良い問題を作っていますね(・・;)
問題①の解答・コメントにおいては、兵庫県と大阪府と京都府を3つの違った色、ア)・イ)・ウ)としてアプローチを進めているのですが、これが、「兵庫県と京都府と滋賀県で進めたらどうなるだろうか?」というアプローチとの違いを理解するところが大切なポイントになることを頭に置きながら、実際に経験してもらえれば『場合の数』に対するセンスやコツを一歩前進させてくれる筈ですよ。
基本的に、『場合の数』の問題はツリー図で整理するにしても、場合分けのモレがないように、一つずつ丁寧に書き出していく作業が全てと言っても過言ではありません。
むやみやたらに問題をこなすよりも、例えば、(1)~(4)の問題だけでも、自分が何故洩らしてしまったのか?を心に刻み込むことを怠らないことの方が大事です。




脳細胞の働かせ方の解説と解答は、ALLコース、中学受験&保護者コースの方は会員専用ページからダウンロードいただけます。
「場合の数のセンスを鍛える精選5題」をダウンロードください。
2番の問題は、「君はラ・サール生になれるか?」で素材にしている問題の「落とし穴の無い頻出標準問題」版です。
違いをよく見比べてください。
3,4番は、ステップアップしようとする君であれば、是非取り組んでおきたい頻出問題です。
5番の栄光学園の過去入試問題は、さすがにユニークで見事な問題ですが、ちゃんと基本を積み重ね、一つ一つの問題から教訓を学び取っていく勉強さえしていれば、それほど難しくない問題です。
たとえ、算数が苦手であるとしても、基本の合間合間にでもこういうレベルの問題を徐々にでも切り崩してこういうことをしないと、脳細胞が繋がるという経験ができないままで終わってしまいます。
それは、使いどころを自分で見つけさせるための時間を入れていくということです。
併せて、小学生の為に「場合の数」を分かりやすく説明した【数学脳への導火線 05-丸竹夷二押御池~場合の数とは?】(PDF14ページ)をご利用いただければ(指導も含めて)、レベルに応じて、なお一層理解を進めることになるはずです。