[脳細胞を働かせてちょう題 04]バルマー系列の規則性を発見せよ!(1)
スイス バーゼルの中学で数学教師をしていたバルマーは、この4本の可視光線の波長情報だけから、この波長の規則性を数式で表現してしまったのです。
この4本の可視光線の波長を表にしますと、下記のようになります。

時間が空いたとき、気分転換したいときに、この4本の可視光線の波長情報だけから、その規則性を数式に一般化してください。

誰も書かなかった高校生向け希望の書

昨年2012年7月に、高校数学の資料として執筆した【物理の天才を閃かせたバルマー先生】の【バルマー系列】が、テレビ放映されている『探偵ガリレオ』で先日登場していたよと知らせてくれた方が居られます。
どうもドラマの事件とは全く関係のない式として書きなぐったとのことですが・・・。
全国広しといえども、
高校生向きに、しかも数学として
この講義がされたことはおそらくないでしょう!
しかし、特に難問題というわけでも全くありません。
その辺の塾・予備校ではお目にかかれない講座をG.ポリアとともにご紹介しましょう!
『探偵ガリレオ』でも意味なく登場したバルマー系列は文系数学で解決しちゃう!
今から書くことは、僕が従来から面白いと思っていた偉人の発見が、どのような脳細胞の動きをもって生み出されたのかを追跡したものです。
そして、大よその脳細胞の動きを推測することができ、また、それが高校生の君たちでも追跡できるものだったので書くことにしました。
それも、ナント!量子論の根幹でありながら文系数学で十分こと足りるんです!
ちょうど夏休みに入ったことでもあり、気分転換やリラックスの意味を含め、少し考える時間を取ってもらえるなら、勉強の面白さと同時に、世の中の大発見も雲の上の話ではなく、面白さの延長線上にあることが分かっていただけることも期待しているのです。
小学生でも解けるかもと暗喩されたフェルマーの最終定理は、実際には数学者でしか解けないほどの高等数学が必要でした。
しかし、今から述べる、前期量子論に大きなヒントを与えることになったバルマー系列の規則性は、今回、「さぁどう考える・・俺? 」という問いかけで僕なりに追求していったところ、高校数学の範囲で辿ることの出来る道だということが分かりました。
ですが、どんな本を見ても「バルマーが気付いた」とだけしか記述されていません。
どうも「根拠は分からないけれど気付いたんだ」というニュアンス以上の説明は見受けられないのです。
以下に僕が書いた追求の大雑把なプロセスを見て、こんな程度で科学の進歩に役立てるのなら勉強するのも悪くはないなと思っていただければ、これ以上のことはありません。
僕が量子論や素粒子論を齧ったのは恥ずかしながら27歳の頃です。
ちょうど最初の会社を辞職し次の会社に転職する合間の頃ですから30年も前の話になります。
学生時代は機械系の工学部でしたから、量子論や素粒子論としては特に勉強する機会はありませんでした。
もっとも、毎日寝に帰るだけで土日も無いほど忙しい状況が慢性化していましたから、せっかくの量子論も素粒子論も、それほど系統化することも無く時が過ぎてしまいました。
勉強したときに、感心したものに、バルマー系列というものがありました。
もちろん、バルマー系列自体は、高校生で習いましたから知っていましたが、それ以上でも以下でもなかったってことです。
最も単純な原子である水素原子から放出される光をスペクトル分析すると、可視光範囲で赤・青・藍・紫4本のスペクトル線が現れます。
「そんな無茶なぁ」と思うかもしれませんが、グラフを描いてみるだけでも、アバウトなら予測できそうやと思うかもしれませんよ。
聞いただけで端からギブアップだと判断するのが多くの子の悪い癖です。
まず、何か行動してみてから判断するようにしてほしいのです。
では、問題をもう少し分かりやすく噛み砕いて表現すると、

なる純粋に数列の問題に帰着されてしまいます。
物理の問題としての意識は全く不要となりますね。
ただ、推論をしていく上でニュートン力学の常識的な知識があれば、無駄な試行錯誤をすることがなくなることは事実でしょうが・・。
これだけでトライしてみたい方は以降は読まないでここで終えてトライに入ってください。
「もう少しヒントが欲しい」という君には、バルマーが結論した答えを先に提示し、与えられた条件と結論を結びつける道筋を考えるという方式で考えてもらいましょう。
要するに、与えられた条件(4つの波長データ)とバルマーが結論した一般式を結びつけてくれればいいわけですね。
さて、
バルマーがこの論文を発表したのは1885年のことですから、まだ量子論が産声をあげる以前のお話。
前期量子論の多大な貢献者ニールス・ボーアはこのバルマーの論文を見た途端に閃き、ボーアの原子模型に結実させたのです。
言い換えれば、バルマーがあってこそ天才ボーアの理論は完結したと言えるかもしれません。
それにしても、バルマーはたった4つの数字の並びを見ただけで、どのようにしてその規則性を数式に出来たのでしょう?
{1,3,6,10,・・・}の規則を予測するのとはわけが違います。
でも、紐解いていくと意外にバルマーの脳細胞の動きがこうだったのではないかということが予測できてしまったのです。
しかも、高校数学の範囲内で・・・。
そして、不思議なことにどんな書籍にもまだ書かれていないのかと思えるほど見当たりません。
「何故だか分からないけど、バルマーは気が付いた」ということになっているのです。

↑OPEN ACCESS終了(PDFファイル16ページ)
クリックで拡大画像↑
あまり詳しく説明すると発見する醍醐味が失われてしまいますので、僕の脳細胞の動きにおける最低限のことを大雑把にだけ説明しておきましょう。
詳細は、「帝都大学へのビジョン」の資料とすることにします。
6月4日:OPEN ACCESS終了(PDFファイル)
購入者の方は、専用ページからダウンロードいただけます。
どこを探しても読めない内容でありながら、しかも、高校数学の基本中の基本「二次関数」を非常に身近に感じることが出来る読み物ですから、是非ご一読くださいね。
脳細胞のステップ1
まずは、数値の変化をイメージとして掴むために、グラフ上にプロットしてみました。
【図を描いてみたか?】というG.ポリアの基本発問の一つは当たり前のように実行されます。
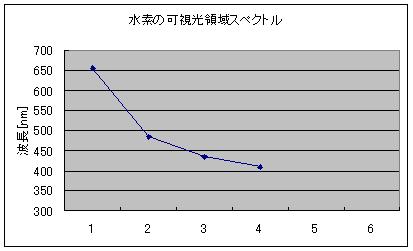
※CADを入れているPCはバックライトが切れてしまい、グラフはExcelで作成したグラフで代替しています。
脳細胞のステップ2
上図のグラフにより、5番目、6番目があったとすればどこにプロットされるのかも、確定しているデータを滑らかに曲線で結び、それを滑らかに延長した線上に乗る点として大雑把な予測はできそうだなと見ます。
ただ、人によってその滑らかさが違ってきますから、グラフだけでは当然正確さに欠けますね。
このとき、横軸は単なるスペクトル線の順番を表す1,2,3という無次元の数であることに対し、「意味がある数字かどうか?」との疑いは当然出ます。
これに関しては、意味があるかどうかは分からないというのがバルマーの出発点であったはずです。
規則性が見つかれば意味があったと結論する以外には表現のしようがありません。
脳細胞のステップ3
とりあえず、このグラフから明晰に言える事は、
- nが大きくなるにつれ、波長は単調に減少し、しかもその減少率(傾き)は小さくなっている。
- 従って、波長はある値に限りなく近づいていくと予想される(漸近値)
そこで、
【こういう性質を持った曲線を知っているか?】なるG.ポリアの基本的な発問をします。
そうすると、該当する曲線で近似するという発想が生まれてきます。
とは言っても、関数で近似するなどは面倒くさいので、出来得るなら、数列として簡単に処理できてくれればという思いがよぎります。
脳細胞のステップ4
それで、とりあえず、数列の要素を素因数分解したり、階差数列を取ったりして規則性を追求しようかと考えます。
当然、関数でやろうとする場合も含めて、小数点などは邪魔ですから、四捨五入した整数でやるわけです。
ところがどっこい、なかなか上手くいきません。
脳細胞のステップ5
そこで、ステップ4はあまり深追いせずに、ステップ3に戻り、ある関数で近似させたところ・・・。
ステップ3で述べた条件を満たす関数はそれほど多くはありません。
君はいくつ挙げることができましたか?
ここで、ニューートン力学でエネルギーと言えば2乗に関連することを想起すれば、これ以外に近似する関数の妥当性は見つかりませんでした。
バルマーの時代にも分かっていたことですから、この点は予想する上でバルマーも想起したかもしれません。
この後、少しセンスが必要なところがありますが、スペクトル線の波長には見事に規則性が存在することを発見できたというわけです。
バルマーの喜びたるや如何ほどだったでしょうか?
その後で量子論として次々と分かってくるわけですが、順番を表す1,2,3という無次元の数は原子の正体を表す数字だったのですね。
純粋に数字だけの分析によって、量子の世界が飛躍的に見えてきたというのも実に興味深いことです。
時には娯楽は必要ですが、アホなバラエティ番組ばかり見たりゲーム中毒にならないで!
一部の大人の策略には乗らない知恵を身につけてほしいのです。
知性を磨かないのはまだいいとしても、何としてでも人としての感性だけは摩滅させないように願います。
2012年7月28日
前の「脳細胞を働かせてちょう題」は、037つの橋の問題
次の「脳細胞を働かせてちょう題」は、05バルマー系列の規則性を発見せよ!(2)