[脳細胞を働かせてちょう題 03]一筆書きの問題?
ある有名な問題です。
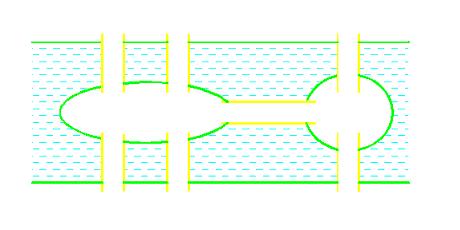
川が流れており、川の中に2つの島(中州)があります。
川の両岸と島には、図のように橋が掛けられており、行き来できるようになっています。
さて、ある地点から出発して全ての橋を1回ずつ渡って、元の地点に戻ることができるでしょうか?
同じ橋を2回渡ることはできません。
この地図をモデル化して、自分の言葉で自分に答えとその理由を説明してみてください。
「モデル化してちょう題!」だって!
実は、この問題には歴とした名前が付いています。
名前を知っているような人なら、すでに考えたことがある人でしょうね。
でも、名前を言っちゃうとすぐに調べて考えようとしないでしょうから伏せておくことにします。
さて、これは、問題を解くというよりも【モデル化してちょう題】という課題です。
「モデル化」なんて、何の意味があるのか?って思われるかもしれません。
が、「モデル化」が出来なければ世の中の問題ってほとんど解決できません。
君たちが将来、情報や数理を扱うデジタルの世界に憧れているのなら、なおさらです。
また、現実的にモデル化して解いていく入試問題も山ほどありますよ。
【帝都大学への過去問着眼点シリーズ】に収録している、2008年京都大学文系数学入試問題問題5が、まさしく、このモデル化ができるかどうかが大きなポイントになる問題でした。
また、同じく収録している某公立高校入試問題にもモデル化が問われる問題がありました。
こういった良問を通じて、「モデル化」は体験することによってしか、その力が養われるものではありません。
「モデル化」って言葉がピンと来られないのであれば、「要点を抽出しイメージ化する」という言葉に置き換えてもらって理解して頂いても結構かと思います。
但し、「モデル化」以前に、どんな問題でも自分が意味を理解するために、一目でわかるようにマンガにしたり、表にしたり、図にしたりする作業をすることが習慣づいていることが前提となります。
「モデル化」というのは、こういったイメージ化の一つには違いないのですが、具体から一般化する力が少し必要になるのですね。
そうなると、大層仰々しい感じを受けられるかもしれませんので、広い意味で捉えれば、日本語で書かれた文章を式や図表やマンガに翻訳して、自分に分かりやすくすることを含めて「モデル化」と考えていただければ結構ですよ。
よく「例えば、順番に書き出してみると・・」みたいに、僕が整理して具体例を並べて書き下している作業だって、「モデル化」だと言えないでもないですから、図形を描くことだって、グラフを書くことだって、広い意味で捉えればモデル化なんだというぐらいの気持ちで読んでいただければ幸いです。
ですから、算数・数学が苦手だ、嫌いだと言われる生徒さんには、まず、問題を自分で見て一目で分かるイメージにしていくことを教えてあげるところから始めてあげなければなりません。
「イメージ化」と聞くと、「右脳」と思われる方が少なくないようなのですが、「右脳・左脳」という言葉自体、今日今すぐに頭の中から”Delete”してください。
浅薄なタレント脳科学者もどきに弄ばれないで下さい。
彼らの物言いで言うなら、左脳を使わないでどうやってイメージ化できるのか聞いてみたいものです。
それでも気になられるようでしたら、「左脳の指令をもとにイメージ化しないと何の意味もありません」とだけは申し上げておきたいと思います。

↑OPEN ACCESS終了(PDFファイル9ページ)
クリックで拡大画像↑
この問題も、小学生でも考えることができますが、説明の仕方が難しい!!
問題をシンプルにモデル化できれば、何の問題なのか?というところが少しは鮮明になってきます。
【脳細胞への導火線】内「モデル化:要点を抽出し可視化すると・・・」にて解説
OPEN ACCESS終了(PDFファイル)
購入者の方は、専用ページからダウンロードいただけます。
ぶっちゃけた話、一筆書きの問題だと見破った方も多くいらっしゃるのではないでしょうか?
一筆書きの問題なら、中学入試問題でもゴロゴロしていそうですね!
そして、実際に沢山出題されています。
【帝都大学への過去問着眼点シリーズ】に収録している、2008年京都大学文系数学入試問題問題5は、まさしく、一筆書きの問題でした。
モデル化して、場合の数を整理していく…そんな問題でした。
本問では、地図のままでは考えにくいことが、モデル化しちゃうと、一筆書きの問題だと分かっちゃうことはもとより、「どういう場合に一筆書きって出来るんだろう?」と考えざるを得なくさえなっちゃいます。
不思議ですね!
「できる奴」とは理系・文系に関係なくモデル化ができる奴
てなわけで、当然ながらとっくの昔に解決済みの結論があります。
オイラーさんっていう超有名な数学者によって解決済みなんですが、だからと言って、別にその結果を教えてもらうことを待たなくても、モデル化さえできれば、自分の頭で予測できますよ。
あるいは、結果を知った後に、何故そう言えるんだろう?ということを日本語で考えて日本語で説明してみてください。
そういった作業こそが、君のセンスを養ってくれますから、是非挑戦してみてくださいね。
ちなみに、この問題は「ケーニッヒスベルグの橋の問題」と呼ばれ、同じ地点に戻ることは許される一筆書きの問題なんですね。
この問題を考えるにあたって、オイラーさんがモデル化したグラフは「オイラーグラフ」と呼ばれます。
「地図だけでも図になっているのに、何をこれ以上イメージ化するの?」と思われるかもしれませんね。
だからこそ、資料にしていますので、是非一読してみてください。
ひょっとして、君も将来、会社の仕事でこれに関わる理論を使って、業務の効率化を図る責任者を命じられるかもしれませんよ!
だって、同じ地点に戻ることも許されない一筆書きの問題も当然あって、これは「巡回セールズマンの問題」(モデル化したグラフは「ハミルトングラフ」)なんて名付けられています。
「効率的に営業するにはどのように回ればいいか?」という現実的な課題そのものなのですからね…。
与えられた問題の要点をシンプルに抽出し、整理し、的を射た解決策を提示していける能力というものは、実は社会人になってからのステータスを決めるとても重要な能力です。
決定的なことを言いますと、世に言う「できる奴」という人々は、理科系・文科系に関係なく、このモデル化ができる人だと言っても過言ではないでしょう。
前の「脳細胞を働かせてちょう題」は、02小野芋子の買い物
次の「脳細胞を働かせてちょう題」は、04バルマー系列の規則性を発見せよ!(1)