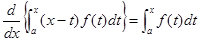 を証明せよ。(
を証明せよ。(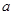 は定数)
は定数)
さてさて、こういう微分と積分が入り混じったものが一番嫌いかもしれないね。
記号を機械的にしか理解していないと、操作方法だけで処理できる計算問題じゃないと、見ただけで手を上げてしまうのかもしれない。
難しそうに見えるけれども実は文系数学レベルだ!
基本は、微分と積分は逆動作であることをまず理解しているかどうかだ。
そんなこと当たり前じゃんと豪語した君。
積分したものを微分したらどうなる?
まず、そこをクリアーしなければならない。
微分して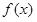 になるような関数を
になるような関数を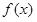 の原始関数と呼ぶというのがそもそもの定義。
の原始関数と呼ぶというのがそもそもの定義。
その原始関数を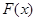 と名付けると、
と名付けると、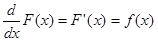 ということになる。
ということになる。
これを、原始関数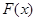 が主語の式で表すと、
が主語の式で表すと、
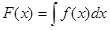 となり、これが一般的な定義式となる。
となり、これが一般的な定義式となる。
当然のことながら、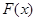 は無数にあることは忘れてはならない。
は無数にあることは忘れてはならない。
(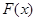 内の定数はどんな数であっても微分すれば消え去ってしまうのだから)
内の定数はどんな数であっても微分すれば消え去ってしまうのだから)
原始関数は不定積分そのものであり、
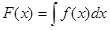 は、微分すれば
は、微分すれば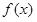 になる関数が
になる関数が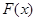 と日本語で読み取るクセを付けておけばいい。
と日本語で読み取るクセを付けておけばいい。
では、問題にある定積分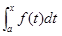 はどういうことか?
はどういうことか?
 の原始関数を
の原始関数を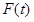 とすると、
とすると、
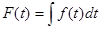
日本語で表現すると、微分すれば になるような関数
になるような関数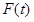 は
は の不定積分である。
の不定積分である。
定積分の定義より、 の
の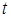 の区間が
の区間が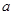 から
から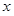 の定積分は、
の定積分は、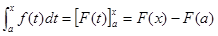
すなわち、定積分は原始関数の区間両端の値の差ということになる。
だから、
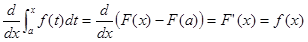
即ち、
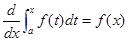 ・・・①
・・・①
なる有名な公式となるわけだ。
この式は、上のような説明を理解した後は、
【 において
において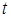 の区間が
の区間が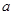 から
から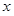 で定積分すれば、これは原始関数
で定積分すれば、これは原始関数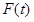 の区間両端での値の差
の区間両端での値の差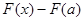 となり、これを実際に
となり、これを実際に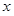 で微分すると、定義そのものによって
で微分すると、定義そのものによって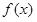 そのものである。】
そのものである。】
といった日本語で意味をしっかり把握しておくと①は実に当たり前の式として暗記などしなくてもスラスラとその場で書けるはずなんだ。
ちょっと乱暴だけれども、『ある関数を積分したものを微分すれば元の関数』というイメージで荒っぽく理解しておいて、実は正確に言うと上のような理屈なんだということを自分の言葉で言えるようにしておけばベストだと思うよ。
さて、この問題は被積分関数に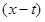 が入っているから単純ではないけれど、難しく考えずに普通にバラして処理してみればいい。
が入っているから単純ではないけれど、難しく考えずに普通にバラして処理してみればいい。
ただ、①の式を覚えているからといって
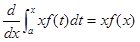 とする諸君が必ずたくさん居るけれども、よーく考えてみてほしい。
とする諸君が必ずたくさん居るけれども、よーく考えてみてほしい。
※会員の方で添削希望の方は画像かPDFファイルでお送りいただければ添削させていただきます。
前の「受験数学 勉強の仕方例」は、偶数次式の着眼点
次の「受験数学 勉強の仕方例」は、頭の中で図を書く訓練



