[共役を知れば作業ラクラク基礎問題]

方程式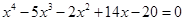x~4-5x~3-2x~2+14x-20=0 において、

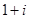  1. 1+i が解であることを確かめよ。
  2. その他の3つの解を求めよ。

[今日の書きなぐりノート]

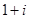x=1+i として、
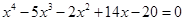方程式x~4-5x~3-2x~2+14x-20=0 ・・・①に代入すればいいだけの話だね！

が、これでは計算が面倒くさいと言うほどでもないけれど、やっぱり面倒くさい！

というよりも、何だかカッコよくはない！

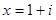x=1+i より x-1=i

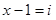
両辺を平方すると、
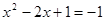
x~2-2x+1=-1

よって、
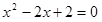
x~2-2x+2=0

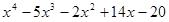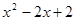さて、x~4-5x~3-2x~2+14x-20 をx~2-2x+2 で割ると、

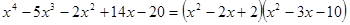
x~4-5x~3-2x~2+14x-20=(x~2-2x+2)(x~2-3x-10)

もう何も言うことはないだろう。

【実係数の整方程式が複素数の解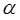α を持つならば、その共役複素数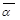α も解である】という定理そのものなんですね。

仰々しく定理だと身構える必要はなく、上の式で解を平方する作業そのもので導かれる。
ただ、一般的な整方程式 が複素数の解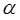α を持つならば、その共役複素数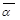α も解であることを証明する手続きは踏んでおいた方がいいね。

もし、解答やいろんな考え方が知りたいと言うならば、以下に会員限定で示すことにしよう。

前の「受験数学 勉強の仕方例」は、次数を減らしてから計算する

次の「受験数学 勉強の仕方例」は、関数の正体を見破る