次数を減らしてから計算する～受験数学 勉強の仕方例講座04

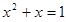を満足する正数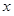に対して、有理数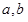を係数とする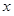の多項式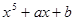
の値が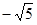になるように、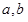の値を定めよ。

問題を素直に紐解いて、言い換えてみよう。

2次方程式、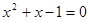・・・・①
の解で正の値をとる解を対象として、

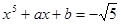・・・②
になるような有理数の値は何か？

という問題である。

①の方程式は、解の公式によってそのまま解ける。
使うかどうかは未定だが手間でも何でもないので、とりあえず出しておこう。

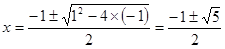
この2つの解の内、正の値をとる解、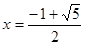 ・・・③
が対象だよ　というお話になる。

③を②に代入してやれば
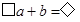という形になって、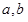が有理数であるという条件から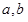は確定されるようになっているのだろうと予測できる。

ただ、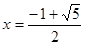 を5乗するなどという計算もかったるい！

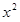なら、①を利用してから出て来ること、
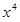なら、これを2乗すれば出て来ることに気付いているだろうか？

どっちにしても僕は、計算はできる限りしたくないなまくら人間だから、次数が高いときにはわざわざ計算をしないことに心を決めている。

では、どうすればいいのか？
五次式の②を二次式①と三次式の積と辻褄が合わない部分を和の形にして表してやればいい。

早い話が、②の左辺を①で割ってやればいいんだよね。
辻褄が合わない部分と書いたのは、割った時の余りの部分のことになる。

二次式①の値は0であるから、積の部分は0になって、余りの部分だけを計算すればよいことになる。
そして、二次式で割ると余りは一次式だよね。

辛―い計算することは何もないよね。

さぁ、やってみてくれたまえ。

もし、解答やいろんな考え方が知りたいと言うならば、以下に会員限定で示すことにしよう。