積分と体積をめぐる基礎問題
3Dプリンターに、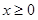 で単調に増加する関数
で単調に増加する関数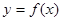 のグラフのデータを入力し、第1象限にある部分をy軸のまわりに回転して得られる回転体が内容積となる容器を製作した。
のグラフのデータを入力し、第1象限にある部分をy軸のまわりに回転して得られる回転体が内容積となる容器を製作した。
これに毎秒a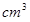 (aは一定)の割合で水を注入したところ、水面の高さがy
(aは一定)の割合で水を注入したところ、水面の高さがy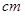 のときの水面の上昇速度は毎秒
のときの水面の上昇速度は毎秒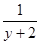
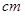 であることが計測された。
であることが計測された。
1) 入力した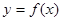 は何であったか?
は何であったか?
2) 水の注入開始からt秒後の水面の高さをtで表してみよう。
ΣとSと∫は親戚だったとは、お釈迦さまでも知るまいよ!
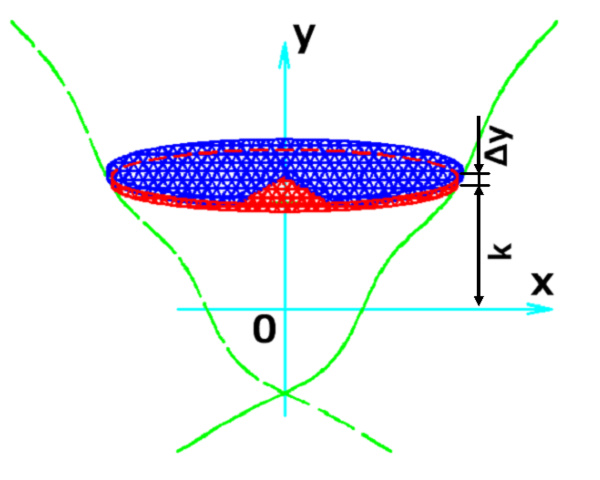
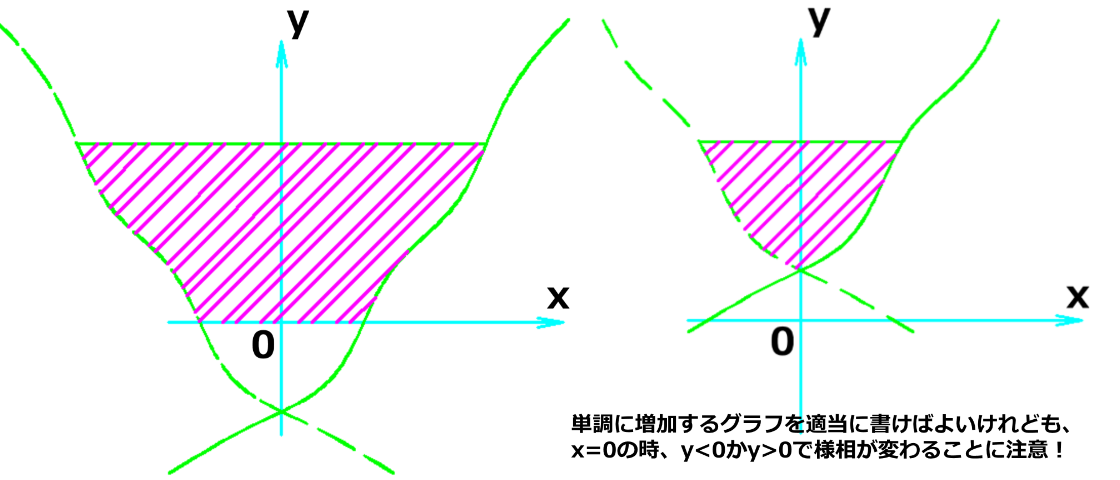
厚みが単調に増えていく(減っていく)ロースハムの塊を左図のようにy軸に串刺しにしてみた。
Y座標がkである断面で包丁を入れ、次に切り口から十分に薄い厚みΔyでスライスして薄いハムを切り出した。(赤いハッチング)
このスライスはy=kでの断面積×厚みΔyの体積があると近似することができる。
(断面積は切り口の両側では違った値であるから誤差が出る)
次の切り口から再び同じ厚みΔyでスライスをすると、これにもy=k+Δyでの断面積×厚みΔyの体積があると近似することができる。(青いハッチング)
この作業を、片方の端からもう一方の端までくり返し、スライスしたハムの体積を全て足せば元々のロースハムの塊の体積が近似できる。
スライスしたハムの体積を全て足す処理を、数学では「SUMを取る」「サメーション(summation)を取る」と呼び、記号はΣ(シグマ)を使うことは知っていることと思う。
技術屋さんや研究屋さんになると、物理データを解析する時などには、「サメーション(summation)を取る」という言葉はよく使うようになると思うから頭に入れておいて!
この記号Σはギリシア文字でSに相当する文字だと聞けば「そうだったのか!」と膝を打つことだろう。
さて、この作業を分析していくと、次のことが分かってくる。
- スライスの厚みΔyを大きくすると、両方の切り口の断面積の差は大きく、従って誤差が大きくなり体積の精度は落ちる。
- 逆に厚みを薄く切れば切るほど、両方の切り口の断面積の差は微々たる程に小さくなり、精度よく体積が求められる。
ただ、いくら薄くスライスしてデジタルの値のSUMを取っても限界がある。
そこで無限に薄く切ったその和をアナログで処理して、正確な値を割り出せないものかと思案する。
これが、『積分』というわけだ。
そして、その記号として∫(インテグラル)が使われることになったが、これはSを上下に引っ張って塑性変形させた形になっているのが分かるだろう。
ΣとSと∫は親戚として繋がっていたのだね。
『積分』という処理は、要するに無限小に分割した値のサメーションを極限の性質からアナログ的に確定することと考えればいい。
高校数学でも、まずは平面上の面積を求めるという処理から学びますが、体積もただ立体と言うだけで考え方は同じです。
微分や積分は意味さえ分かれば、高校数学程度では単純作業の最たる単元ですから、怖がらなければ得点源にできますよ。
今日の書きなぐりノート
1) 分かっていることを書き出す
体積を V とすると
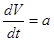 ・・・①
・・・①
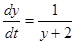 ・・・②
・・・②
時間によって変化する物理量を扱う場合は、変量を時間で微分することが基本になります。
与えられた条件を、上の①、②の式として書き出せることは基本中の基本です。
さて、体積とはy軸に垂直に切った断面積を0からyまで積分したものであり、(x,y)座標点がy軸のまわりに回転して作る断面は円であることから、
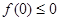 の場合、
の場合、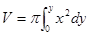 ・・・③
・・・③
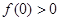 の場合、
の場合、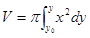 ・・・④
・・・④
③の両辺を時間tで微分すると、
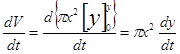 ・・・⑤
・・・⑤
④の両辺を時間tで微分すると、
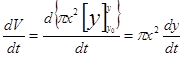 ・・・⑤
・・・⑤
①、?を⑤に代入すると
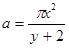 ⇒
⇒ 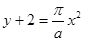 ・・・⑥
・・・⑥
よって、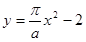 ・・・解答終了
・・・解答終了
2) t秒後までに注入された水の容量はat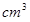
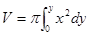 ・・・③がatと同値になったときのyがt秒後の水面の高さとなる。
・・・③がatと同値になったときのyがt秒後の水面の高さとなる。
⑥により、t秒後までに注入された水の容量は、
・・・
次の「受験数学 勉強の仕方例」は、素因数分解・互いに素








