よく出る面積の基本問題～算数：過去問で基本を鍛える(13)

過去入試問題より・・・よく出る面積の基本問題

今回も特定の中学校の入試問題というわけではなく、入試にもよく出題される面積の基本問題で鍛えておきましょう！

このような基本的な問題の考え方をしっかりと経験しておけば、なんか難しそうな問題でも、いろんな手掛かりを探り出す力が身に着きます。

「長方形を対角線で切ってやれば、同じ三角形ができる」
たいていの子は、そんなことは当たり前と言うのですが、この当たり前のことが問題に組み込まれると、まったく気が付かないんですね。

目の付けどころ＆知っておくべきこと

まず、問題の図を見て「なーんだ！」って思う子は、もう手慣れたものなんだろうね。

逆に言えば、問題の図を見て、すぐに「何をするのか？」が分かってしまうかしまわないかで最初から差がついちゃうということになる。

たとえ塾に行っていなくても普通に解くことができるようになると思うよ。

だって、僕の教えた子は、塾に行っていなくて学校の授業以外のことは何にも知らなかったけれど、ああやったりこうやったりで一生懸命工夫してたいていは自力で解き切っていたからね。

下図で台形ABCDの面積を求めなさい

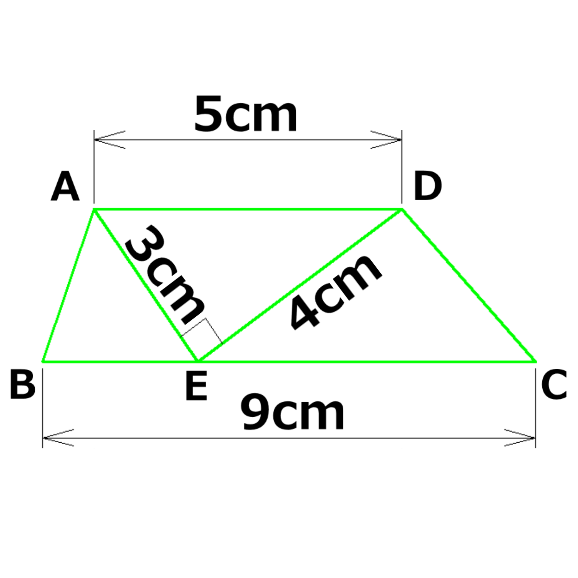
高さが書いてないじゃん

直角三角形の面積は分かるんじゃない？

上の図のように高さの線（赤いたての線）を描いたら気が付いたよ

それに下の図のようにAとDから高さの線を2本描いたらね、
高さを求めなくても面積が出ることに気付いちゃった！
下図で四角形ABCDの面積を求めなさい

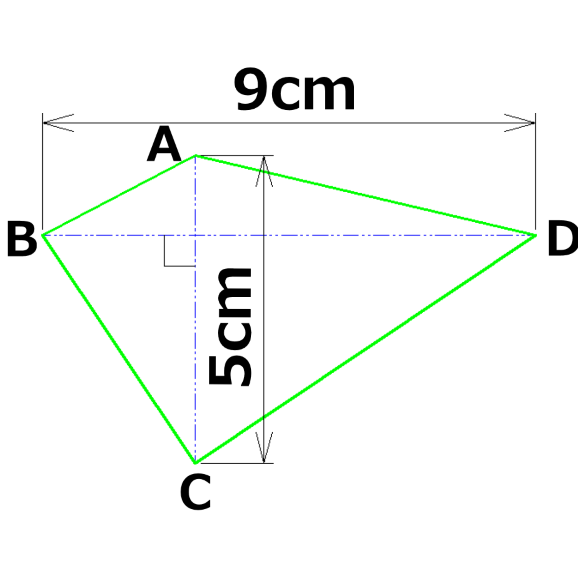
こんな四角形の面積の公式ってあったっけ？

たての横の線が入ってるから、4つの三角形の和だと
知らせてくれてるのかしら？

たての線と横の線がヒントだったぜ
四角形を囲むように長方形を描いたら、一発で分かったよ！

対角線が直角に交わる四角形の面積は、「かけて2で割れ」
って教わったけど、今ようやく意味が分かったよ！
下図で三角形ABCの面積を求めなさい

こんなの全然習ってないよぅ！

30°に何か意味があるのかな？

おぉ！隣あわせに同じ30°の三角形を作ったら、
正三角形ができちゃって、上の2番の問題と同じになっちゃった！

30°って出て来たら、同じものを作って60°にすれば
謎が解けるかもってことをもう忘れないと思うぜ！
正方形ABCDの面積は20cm²です。正方形EFGHの面積を求めなさい

でっかい正方形の面積だけで、どこの長さも書いてないじゃん

でっかい正方形の１辺と円の直径は同じで、一番小っちゃい正方形の対角線が、やっぱりこれと等しいから、とりあえず直径と対角線の線を描いておこうかな

対角線EGを１辺とする正方形を作ったら、
これって正方形ABCDと同じ大きさ、同じ面積じゃねぇ？

これだと大きい正方形の面積の何分の1かって分かるじゃん！
ブラボー！！
下図で、ピンクの網目の部分の面積を求めなさい

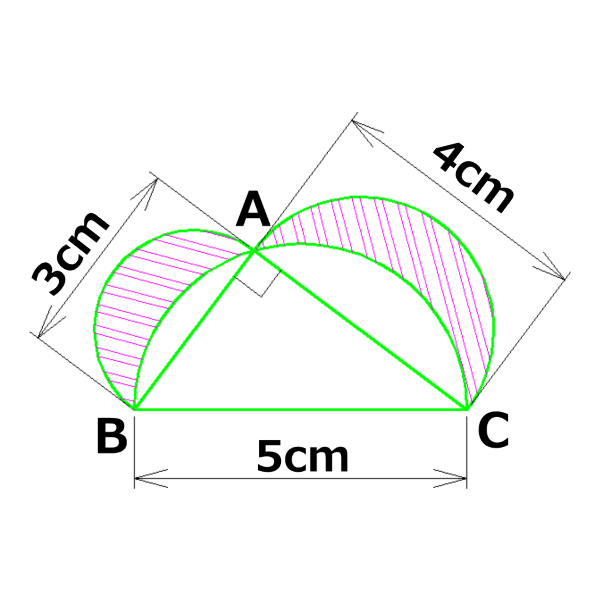
なんだかややこしそうだなぁ！

でも、全体の面積は直径3cmの半円と直径4cmの半円と
直角三角形の面積をたせばいいんだよな

その全体の面積から、直径5cmの半円の面積を引けば、
ピンクの網目の部分の面積じゃん

素直にコツコツ計算すればいいって話か！

でも、この2つの三日月の面積の和だから、少数点が出て来るのかと思ったら、きれいな整数で、しかも直角三角形の面積と同じになっちゃってビックリ！

実は、そのことは「ヒポクラテスの定理」って呼ばれていますよ。
君たちが中学3年生以上になった時に分かることなんだけれど、
「ピタゴラスの定理」っていう真実から考えれば当たり前だったんです！
中高生になるのが楽しみだね！