過去入試問題より・・・よく出る角度の基本問題

今回も特定の中学校の入試問題というわけではなく、入試にもよく出題される角度の基本問題で鍛えておきましょう!
と言うか、二等辺三角形・正三角形の問題なのですがね…。
下のような角度を求められる問題は、重なり合っている図形の中に二等辺三角形やら正三角形やらの単純な図形を見つけさえすれば、芋づる式に分かってしまう問題が多いのですよ!
「ウォーリーを探せ」的な頭のお遊びも、こういった能力に寄与してくれるかもしれませんね。
算数の基本を鍛える問題2題と目の付けどころ&知っておくべきこと
図形に関する問題の場合、まず、問題を読んで、
- 問題に書いてある文から分かることを図に書き込んでいく
- 何か特徴的で単純な図形がないかどうかを探す
特徴的で単純な図形とは、名前を持った図形であり、たとえば、たいていは、
- 二等辺三角形・正三角形・直角三角形
- 正方形・平行四辺形
- 合同や相似になっている図形はないかどうかを探す
- 単純な図形の特徴や合同・相似の性質から言えることを図に書き込んでいく
- 同時に、計算すれば出るような角度も書き込んでいく(三角形の内角の和は180°)
という流れで進めていけば、かなりのことが見え始めます。
先ずは、下のような基本問題で、その作業をササッとできる訓練をしてください。
もちろん、その前提として、たとえば、「二等辺三角形は2つの辺の長さが等しい」だけではなく、「二等辺三角形は二等辺に向き合う2つの角も等しい」ということが反射的に出て来なければなりません。
そして、すぐに図の中にチョンチョンと「こことここは同じだよ!」てことを書き込むクセをつけてくださいね。
-
一つの辺が共通な正方形と正三角形が描かれた下図で\(x\)°を求めなさい。

文章から分かることを素直に図に書き込む!



他に暗算ですぐに出るような角度も書いておく(頭に入れておいてもいい)
単純で特徴的な図形や合同・相似な図形は見つかったかな?

見つかったかならば、その特徴や性質から言えることを書き込んでいく -
下図で四角形はABCDは正方形で、AE=ADです。\(x\)°を求めなさい。
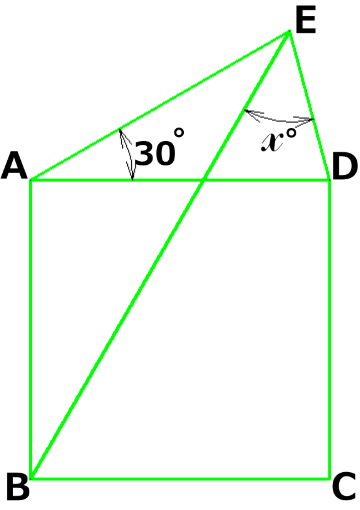
文章から分かることを素直に図に書き込む!



他に暗算ですぐに出るような角度も書いておく(頭に入れておいてもいい)
単純で特徴的な図形や合同・相似な図形は見つかったかな?

見つかったかならば、その特徴や性質から言えることを書き込んでいく -
下図でアからクまでの8つの角度の和を求めなさい。
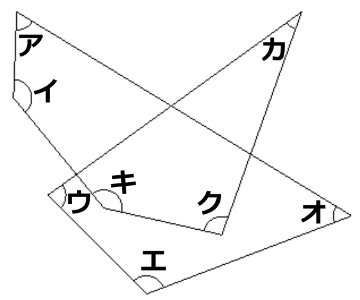
この問題は、超難関中学から中堅中学の入試でもよく出る問題の変形です。
同じ図形なんて出ませんから、図が違うから分からなかったなんて言わないようにしてください。
正直な話、本当にできる子は、中堅校受験生でも瞬即数秒でできますが、超難関校受験生でもできない子は最後までできません。
- 三角形の内角の和は180度であること、四角形の内角の和は360度であること。
- 五角形以上の多角形の内角の和は決まっていて、三角形や四角形に分割すれば、すぐに割り出せること。
- 対頂角は等しいこと。
たかだか、この3つの基本を知っていればできるはずなのにです。
この問題が解けないという場合は、あちこちに転がっている塾の解説を聴いているだけでは効果が期待できないかもしれませんね。
要するに、問題と自分の基本知識を結びつける回路が、訓練によってできていない、しかも教訓として刻み込まれていないということが元凶にあります。
いい機会ですから、できる限り考えるようにしてみて下さい。
もっと根元に言及しておきますと、「こんなのおかしいや!」「こうだったら分かるのにな!」という思いが乏しいか、これを燃焼させて解決する術を見出せないという点が合格者との決定的な差になっています。
よく出る台形の面積比~算数:過去問で基本を鍛える(12)もチェック!!
よく出る面積の基本問題~算数:過去問で基本を鍛える(13)もチェック!!
有名過ぎる面積問題9題と灘中学過去問題1題+考えすぎない1題~算数:過去問で基本を鍛える(20)








