過去入試問題より・・・よく出る台形の面積比

今回は特定の中学校の入試問題というわけではなく、入試にもよく出題される台形に関する面積比の基本を鍛えておきましょう!
よく「台形面積は公式を覚えなくても大丈夫」といった記事が多く見られますね。
確かにその通りなんですが、それほど仰々しいことでもないような気がします。
図形を見ただけでイヤになる子も多いかもしれませんが、「やってみれば意外に簡単じゃないか!」と感じるところから自信は生まれてきます。
簡単と難しいを橋渡しするような問題ですから、是非、じっくり理解するまで粘ってください。
お子さんが変わるのは意外に、たった一つの感動や達成感からであることが多いものです。
塾の講義を「フーン!」と頷いて終わっているだけなら全く意味無し。(勉強の本質です)
算数の基本を鍛える問題(12)

【問題】
左の図で(ア)の部分と(イ)の部分の面積が5:3のとき、DE:ECの比を求めなさい。
目の付けどころ&知っておくべきこと
まず、問題の図を見て「なーんだ!」って思う子は、もう手慣れたものなんでしょうね。
逆に言えば、問題の図を見て、すぐに「何をするのか?」が分かってしまうかしまわないかで最初から差がついちゃうということになります。
「塾に行ってないから僕には分かんないよ!」という子は、次のように考えてみればどうかな?
別に、塾に行っていなくても普通に解くことができるようになると思うよ。
私たちは、そのことこそを望んで、中学受験のコンテンツを追加しています。
だからこそ、それぞれの子どもの反応に応じた起点から、正解にはたどり着けないアプローチも含めた脳細胞の動きがあれば、それをネタに指導を進めることを信条として来ました。
本当は、正しい道筋(いろいろ考えた末の結果でしかありません)をエラそうに教えられても、しかも口だけで言われても、ある意味「フーン」で終わってしまうのは当たり前だと思いますよ。
なんとなく塾に行かせているけれど、成績が一向に伸びない場合は、ここが完全に欠落しているから。
しかも、耳で聞いたことほど虚ろなことはありません。
耳で聞いたことは、その日の内に自力で再現する時間を取らないことには、その日に宙に消えて終わりです。
-
(ア)の部分の台形は変な形で面積なんてお手上げだから何か線を引いてみよう!
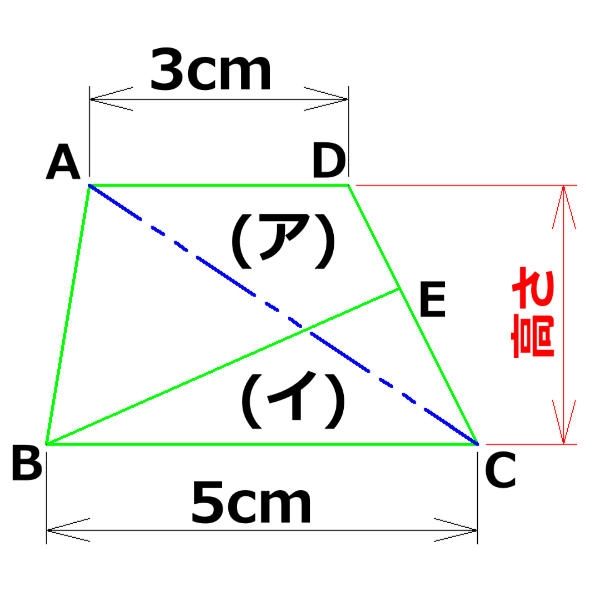
(ア)の部分の台形を見ていてもらちが明かないや!

何か線を引けば分かるんかな?

AとCを結んでやれ~!

変な四角形が小さくなっただけで余計に分かんないや!

こんな線を引いても、何にも解決しそうにないぜ! -
他に引ける線は?っと…
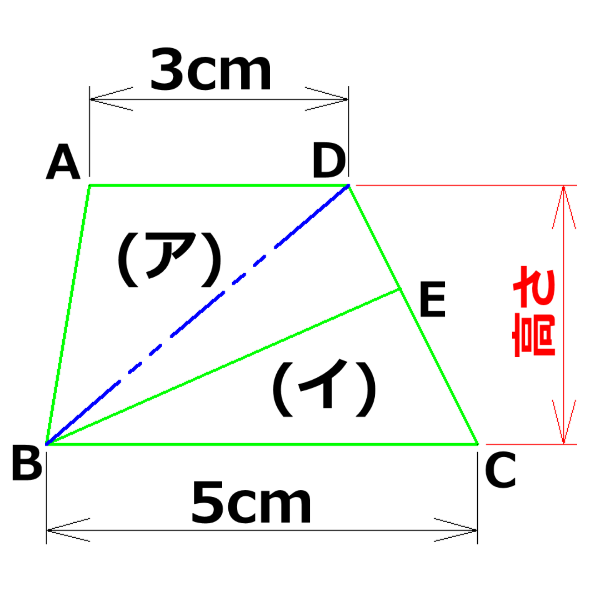
BとDを結んでやれ!

おっ!変な四角形は消えて全部が三角形に分割されたぞ!

(ア)の部分の面積は三角形ABDの面積と三角形DBEの面積の和になっている!

それに、三角形ABDと三角形BDCは底辺が3cmと5cmで違うけれども高さは同じだぜ!

ということは、面積の比が3:5ということじゃないか! -
問題にある線分BEは三角形DBCを2つに分割する線になってる!
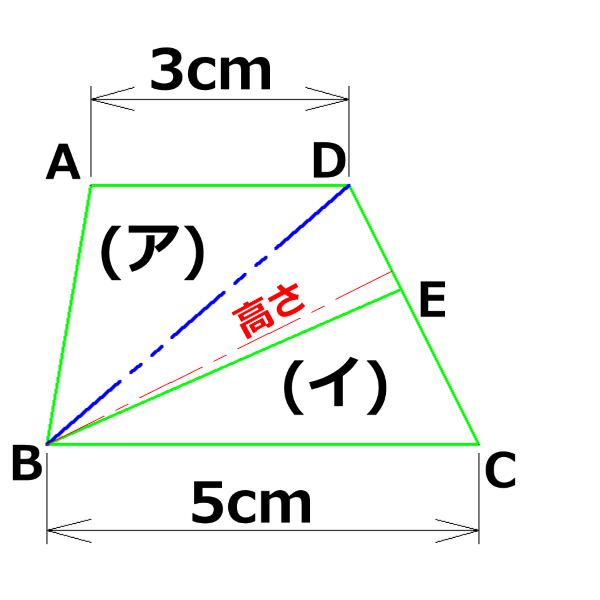
三角形DBEと三角形CBEも底辺がDEとCEで、面積を計算するときの高さは同じじゃないか!
-
高さが同じなら面積の比は底辺の比と同じ!
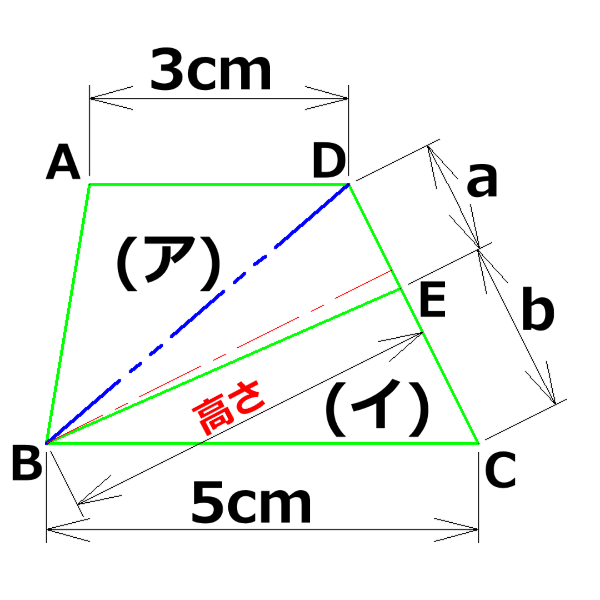
三角形DBEと三角形CBEの面積の比はDE:CE、すなわちa:bと等しいということだ!
-
多角形の面積も三角形に分割して考えると見えてくる!
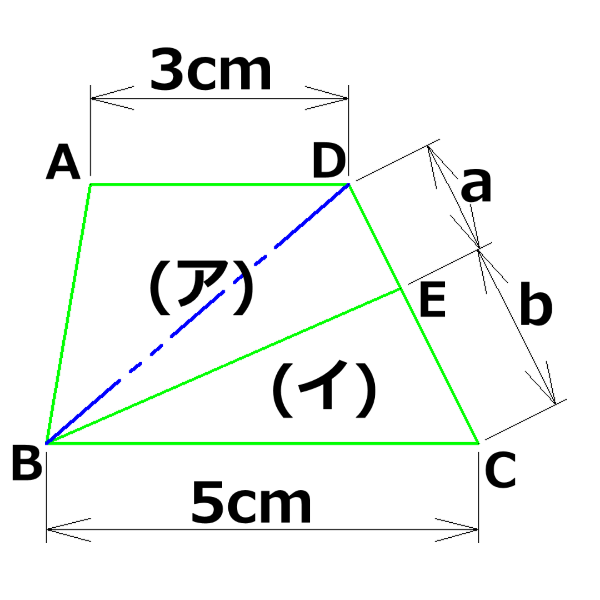
2.の結論からは、全体の面積を8とすると三角形ABDが3で三角形DBCが5ということ。

問題から、(ア)の部分と(イ)の部分の面積は5:3だから、これもちょうど全体の面積を8とすれば、(ア)が5で(イ)が3。

ということは、三角形DBEが2で三角形EBCが3ということになる。
この問題は、考えるプロセスと理由を大切にするために、全体の面積を8として統一して考えられるように比を設定してあります。
私の場合は、「全体の面積を8とすると」で済ませてしまいますけれど、実際問題としては、全体の面積を1として統一し、配分は分数で表現した方が印象が良いと取る学校もあるかもしれません。
上の問題では、全体の面積を1とすると三角形ABDの面積は\(\frac{3}{8}\)で三角形DBCの面積が\(\frac{5}{8}\)という表現ですね。
台形や多角形の面積は2つの三角形に分割して考えれば正体が見えてくることが多い!
今、こころに刻んでおいてくださいね。
でもね、たいていの子は「そんなことは知ってる!」と仰るのですよ。
真面目に一応勉強をしている子は、確かに知っているのですが、実際の問題で使えない、と言うより、使う土俵にまで、ただ進んで来れないんですね。
まぁ、支度部屋で「俺、怖いから行きたくない」とダダをこねているのと同じ状態かもしれません。
そこのところが、指導者の入れるべき最も大切な力点なのですがね…。
優等生の正解を、ダジャレを入れて一方的に解説されるのがほとんどではないでしょうか?
最後に、下の問題を確認しておいてください。
上の問題より簡単で、中堅校以上を目指しておられるなら取りこぼしできないような問題ですが、考え方をより確かに掴むために1ステップずつ確かめながら進めましょう。
パターン暗記しているだけで、自分の言葉で、きちんと説明しながら解答を書いていけないのであれば、中高生になると必ず成績が落ちていきますよ。
さらに、次の2点についての関りについて見直して理解しておくと、鬼に金棒です。
- 三角形を無理に作らなくても、分割された小さな台形(上辺と底辺が平行)にはそのまま台形の面積の公式が使えること
- 逆に、台形の面積の公式は三角形に分割すればその理由が説明できること

【問題】
左の図で線分DEは台形の面積を二等分しています。BEの長さを求めなさい。
「台形の面積の公式を三角形に分割して即座に説明できる」ところまでやってみる勉強の仕方をした子なら、この問題は5秒で答えが出ます。
体験してみる面積問題の天国と地獄!
最後に、下の力試しの問題にトライしてみてください。
どうやら、会員の生徒さんも悪戦苦闘されているようですので、考え方を簡略に資料化したものを会員様限定でアップいたしました。
面積問題の1つのシーンですが、一般的には如何に事務的で断片的な教わり方しかしていないのかも感じてしまわれるかもしれません。
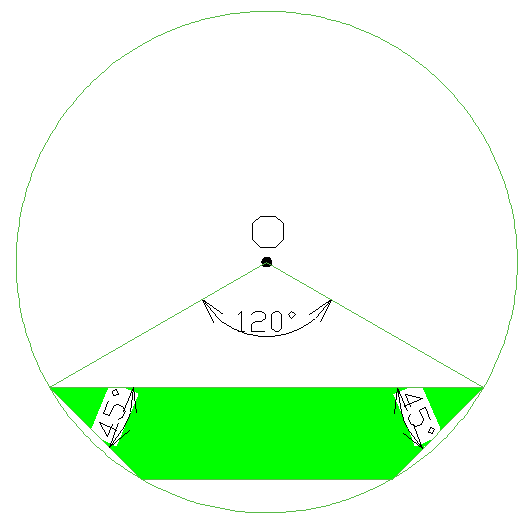
【力試し問題】
右図の緑色で塗りつぶした台形部分の面積を求めなさい。
円Oの半径は8cmとします。
画像クリックでもう少し大きく見れます。
【ヒント】
- 考えすぎるとドつぼにはまります!
- とは言っても、考えないと手が出ませんし、考えすぎる子の考えの中にもヒントがあります。
- 有名過ぎる面積問題9題と灘中学過去問題1題の中の1題にもヒントが隠れています。
- この図形を紙ベースで印刷して、そこに書き込んでいかないと、頭の中だけではまずできないと思いますよ。
- 杉下右京なら多分こう言います。
「ここには紙と書くものがないので何とも推測だけで申し訳ないのですが、おそらく論理的には、面積は・・・になるはずです。だって、「円周率は3.14で計算してください」などの説明は書いていないですからねぇ。」 - 堂々巡りをしてると思ったら、できるだけ早く、「そのときには、いったん、ふんぎりをつけること」を覚えてください。
【正直な話】
塾にも行っていない子が、ものの2,3分ほどで解きました。
信じられないかもしれませんが、本当の話です。
「変な既成概念を持たない子=考える力がある」と言えるかもしれず、優等生過ぎる子には弱点をさらけ出してしまうかもしれない問題です。
【注意事項】
よく、「小学生に正三角形の面積を出す方法をどのように教えたらいいか?」「小学生に√を教えるにはどのように教えればいいか?」などのご質問されている保護者さんが見受けられます。
そんなことは教える必要もなく、むしろ、正三角形の面積は小学生では高さを示されない限り出すことはできないことを教えておくことの方が大切です。
小学生の頃から意味もなく暗記させても何のご利益もないことは断言しておきましょう。
むしろ、この問題を、少しずつ出来る限りまで考えさせる方が、はるかに脳にはご利益があります。
1日、間をおいて、気分を一新して新しく考え直そうとする経験を教えることこそが大切なことです。
本当は、そういうことまでアドバイスしておいてあげないと指導にはなっていない入試問題レベルですから、塾に行っていない子の方が解けちゃうなんてことも起っちゃうのでしょうね。
「もし正三角形の面積を出さないと答えが出ないじゃん!」というところで行き詰ったら、必ず、他に仕掛けがあると仕切り直すことを教えておくと、むやみに堂々巡りの思考をすることをやめて、考える方向を切りかえさせられる可能性を高くすることでしょう。
よく出る面積の基本問題~算数:過去問で基本を鍛える(13)もチェック!!
よく出る角度の基本問題~算数:過去問で基本を鍛える(17)もチェック!!
有名過ぎる面積問題9題と灘中学過去問題1題+考えすぎない1題~算数:過去問で基本を鍛える(20)
「体験してみる面積問題の天国と地獄!」の1題と「基礎を鍛える10題」のうち関連が深い1題の解説(脳細胞の動き)を「面積のセンスを鍛える一つのヒント」(PDF7ページ)としてアップいたしました。
算数だからこそ日本語で理解し納得しなければ、いつまでたっても苦手は克服できないことを、ここでも感じていただきたいと思います。
対面指導ができれば盤石なのですが、どこかで事務的で片手落ちの説明を受けるよりは、はるかに有益だと思いますよ。