東洋英和女学院中学・麻布中学etc～算数：過去問で基本を鍛える(8)

麻布中学・東洋英和女学院中学過去入試問題より・・・タイプに分ける智恵

東洋英和女学院は関西の私にはあまり知る由もないのですが、よく名前の通っている学校だという認識はあります。

どうやら、麻布中学とその源は同じところにあるようですね。

麻布中学は、私たちの時代から「東の麻布、西の灘」と評されて来た超進学校です

小学校時代の同級生が、もともと関東の方だったのでしょう、ちょうど中学で東京に帰られることになり麻布に合格された話を聞いたことを思い出しました。

さて、下の問題は、サイコロの目の数の和に関する問題です。

(1)は六甲学院中学、(2)は麻布中学、(3)(4)は東洋英和女学院の問題です。

君も知っているように、サイコロの目の数は向かい合う目の数をたせば、どの面をとっても7になります。

このことを利用して解いてくださいという問題ですね。

これも、いろんな考え方があると思いますから、各自よーく考えてみて下さいね。

日本語でうまく説明できたなら、よかったらコメント欄で説明して下さい。

算数の基本を鍛える問題(8)

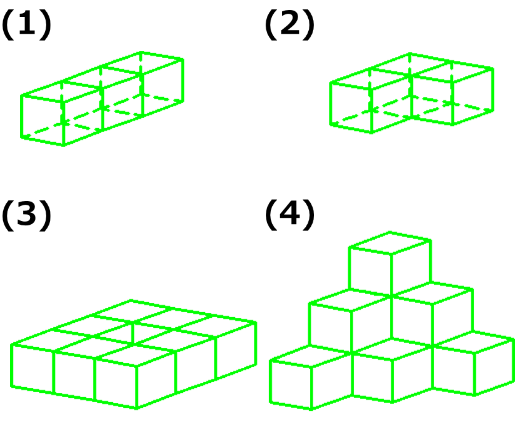
東洋英和女学院中学過去入試問題サイコロ

向かい合う面の和が7のサイコロを次のように並べ、表に出ている面の数の和を最大にするとき、その和を求めなさい。
ただし、立体の底の面も数えることにします。

また、(3)は真ん中が空洞になっています。（空洞部分に縦の線が見えますから判断できますが、実際の問題は空洞部分をハッチングして空洞であると説明されています）

目の付けどころ＆知っておくべきこと

小問の(1)と(2)を考えていくときに、この問題がどういう問題なのかという意味をとらえましょう！
- 実際問題としては、東洋英和の問題には(1)と(2)がありません。
  (3)が小問の役割をはたし、(4)の問題を解かなければなりません。
  東洋英和恐るべしです！
- もし、(3)からして分からない場合は、(1)や(2)の問題を自分で作って考えてみればいいんです・・・小さい数で考えるというクセがついていれば自然にそう考えますよ。
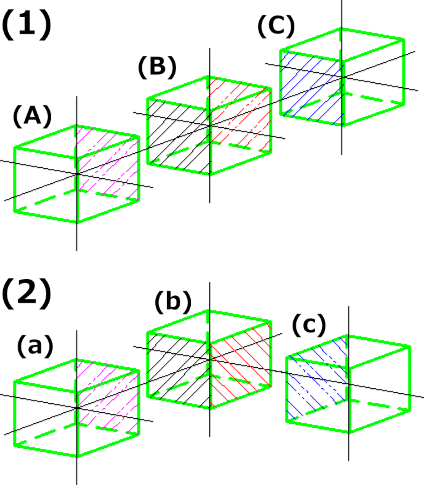
(1)と(2)を右の図のように、ちょっと分解した感じで考えてみると、
- (1)は1列に3個並んでいる単純なケースだね！
  ちょうど串で突きさした三色団子に似ている
- それぞれのサイコロで見えない面を斜め線でハッチングしてみた。（隣にサイコロがある面だね。）
- ここで、3つのサイコロの様子が違うことに注目して欲しい。（何かが違うことはタイプが違うということとして、どれだけのタイプがあるのかを整理する必要があるということだよ！）
- 両端のサイコロは向かい合う2つの面が2ペア見えていて、向かい合う2つの面の片方しか見えない面が１ペアあるね。
- ところが真ん中のサイコロは、向かい合う2つの面が２ペア見えているところは同じだけれど、もう一つの向かい合う面は両方とも見えないね。
- 明らかに、両端のサイコロは同じタイプだけれど、真ん中のサイコロはタイプが違うと言える。
  - 両端のサイコロ：向かい合う面が両方とも見えるのが2ペアと向かい合う一方だけが見えるのが1ペア
  - 真ん中のサイコロ：向かい合う面が両方とも見えるのが2ペアと向かい合うどちらも見えないのが1ペア
- だから、それぞれのサイコロで見える数の和は、
  - 両端のサイコロ：7×2＋（1～6の中のどれか）
  - 真ん中のサイコロ：7×2
- 見える数の和を最大にしたいというご要望であれば、（1～6の中のどれか）に6を入れるしかない！
  - 両端のサイコロ：7×2＋6＝20
  - 真ん中のサイコロ：7×2＝14
  - 合わせると、20×2＋14＝54
- (2)は1つのサイコロを角にした並び方！
- (1)と同じように、それぞれのサイコロで見えない面を斜め線でハッチングしてみた。（これも隣にサイコロがある面だね。）
- 明らかに、両端（角以外）のサイコロは同じタイプだけれど、角のサイコロはタイプが違うと言える。
  - 両端（角以外）のサイコロ：向かい合う面が両方とも見えるのが2ペアと向かい合う一方だけが見えるのが1ペア
  - 角のサイコロ：向かい合う面が両方とも見えるのが1ペアと向かい合う一方だけが見えるのが2ペア
- だから、それぞれのサイコロで見える数の和は、
  - 両端（角以外）のサイコロ：7×2＋（1～6の中のどれか）
  - 角のサイコロ：7×1＋（1～6の中のどれか）＋（1～6の中のどれか）
- 見える数の和を最大にしたいというご要望であれば、（1～6の中のどれか）に6を入れるしかない！
  ただ、角のサイコロの場合、2ペアあるけれど、見えるサイコロの目が同じであることはあり得ないので、一方には6、もう一方には5を入れるしかない。
  - 両端（角以外）のサイコロ：7×2＋6＝20
  - 角のサイコロ：7×1＋6＋5＝18
  - 合わせると、20×2＋18＝58