問題を読んで、「さて何をしようか?」と着眼点を拾って方針を立てたところまでの脳内の動きだけをご披露しました。
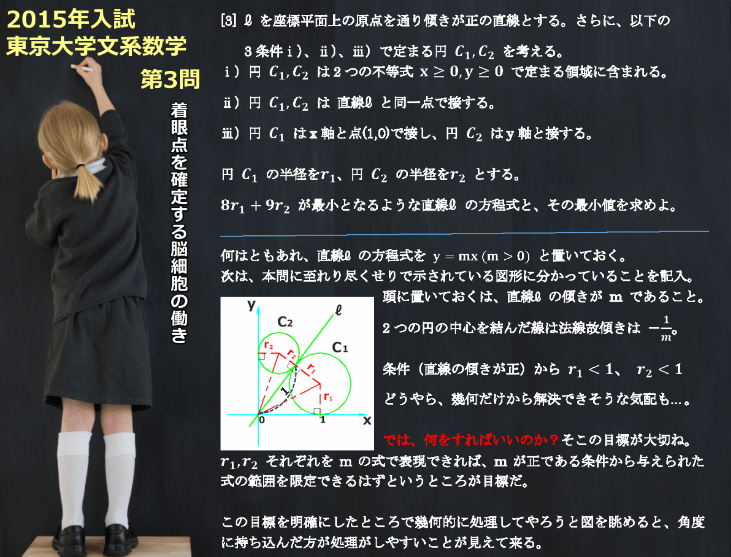
ご親切に図まで問題に示されているから意味的にはしっかり把握できる問題だよね。
非常に単純な構図なので幾何で解けちゃう大したことのない問題だと思ったけれど、第一印象程甘くはないようだ。
ともかくも、図にきっちり分かっていることを記入しながら、意味合いを考え何をしていくかの目標を明確にしなければならない。
r1とr2を直線の傾きmで表現できれば簡単と思ったけれど、式を書きなぐると結構面倒くさい。
こりゃぁ方針変えた方がいいかもと、図を眺めていると、90度の範囲に合同を持つ三角定規が2種類。
こりゃ角度の方だと思った瞬間、何のことはない、tanθ=r1そのもの。
r2もθを使って表せるじゃん。
まさに三角関数で処理できちゃう。
処理しているうちに相加相乗の不等式に出会うことになるけれど、ここで完全にゴールが見えてきた。
あとは事務処理。
■着眼点を確定する脳
- 図を描き、分かっていることは記入しておく。(同じ角度だとか、決まっている数値だとか)
- 何をしなければいけないのかの目標を明確にすること。
- 少し歩を進めた方法がややこしそうだとか面倒臭そうだと不審に感じたら、一旦置いて、他の方法を模索してみる。
- 直線の傾きは代数的表現ではmだが、幾何的表現ではtanθ。
同じことを違った側から見て「どっちが無駄がないか?どっちがスマートか?」と比較することを普段から心掛けておく。
この問題はシンプルそうに見えて、そこそこ手間が必要だろうね。
合否ラインの差をつけるにはちょうどいい問題かなという気がする!