
Q1: 問題を理解しましたか?
QP11:未知のものは何か?・・・三角形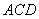 の面積の最大値!
の面積の最大値!
QP12:与えられた条件は何か?
・・・①座標平面上に4点.jpg)
.jpg) 、
、.jpg)
.jpg) がある。
がある。
②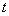 は実数で
は実数で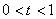
③点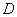 は
は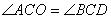 となる線分
となる線分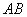 上の点
上の点
QP14:与えられた条件は十分か?不十分か?矛盾はないか?
・・・まぁ、多分これで十分じゃねぇ!
図を描いてもう少し進めなきゃ分かんねぇぜよ。
QP14:図を描いてみれば理解できそうか?
・・・与えられた条件をそのまま座標平面に上にプロットするのは簡単ね。
幾何学的に解けるんじゃねぇーの?
まぁ、そんなことはどっちでもいいか?
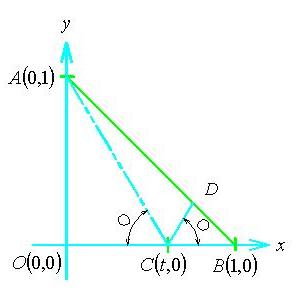
言えることは、最終は三角形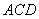 の面積だから、点
の面積だから、点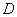 の座標を求めることが必須だということね!
の座標を求めることが必須だということね!
.jpg) は
は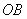 上の全ての点を取り得るけど、点
上の全ての点を取り得るけど、点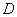 の座標は、この図から見る限り大して難しくもなさそうだから、この絵から三角形の面積を式的に導くのが常道じゃねぇ?
の座標は、この図から見る限り大して難しくもなさそうだから、この絵から三角形の面積を式的に導くのが常道じゃねぇ?
QP15:新たに導入するべき記号はあるか?
・・・あるとすれば、点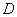 の座標だけど、2直線の交点座標だから、わざわざ新しい記号を与
の座標だけど、2直線の交点座標だから、わざわざ新しい記号を与
えてやる必要もないだろう。
QT11:それよりも、もう少し図から言えることを書き出しておこう!
・・・直線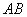 の方程式は、
の方程式は、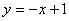 ・・・①
・・・①
直線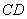 の方程式は、
の方程式は、
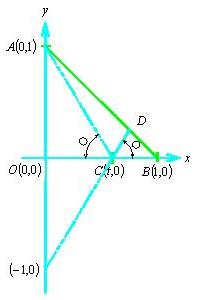
おっ!これこそ幾何的に一目瞭然だわ。
○の角度が等しいという条件だから、
直線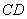 を延長すれば、右の図のように、明らかに
を延長すれば、右の図のように、明らかに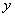 切片は
切片は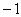 になるもの。
になるもの。
直線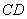 の傾きは、
の傾きは、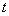 進んで
進んで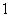 増えるから
増えるから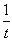 てなわけで、
てなわけで、
直線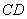 の方程式は、
の方程式は、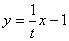 ・・・②
・・・②
①と②の交点を出せば、それが点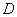 の座標だわさ!
の座標だわさ!
あとは、三角形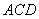 の面積を求めることができるかどうかだけ確かめておくか!
の面積を求めることができるかどうかだけ確かめておくか!
3点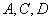 の座標が分る →
の座標が分る → 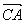 と
と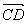 の成分が分る → 確か公式があるよな!
の成分が分る → 確か公式があるよな!
2次元平面だから、ややこしい方の公式なんか要らんわい!
もう、計画はできてしまったわ! 後は、実行あるのみ。
※通常の勉強の際なら、いろんな面積の求め方にトライして頭を整理しておこう!
多分、東大受験生クラスになると「外積」の概念からも公式を理解していることと思うけれど、恐れることは何もない。
君が知っているややこしい公式(内積表現型)に成分を落とし込めば、結果は、当たり前のことながら同じ公式になる。
そのややこしい公式は、面積の当たり前の基本からすぐに導き出せるものだから、必要に迫られたとしても、導出できるという自信をつけておくために、理解できるまで再現しておいて。
Q2: 計画を立てることができましたか?
・
・
・
図を描き、必要なことを書き出していけば、計画を立てること自体は難しくない問題ですね。
君も東大に行ける理由が分ってもらえたでしょうか?
教学社
志望校攻略に欠かせない、大学入試過去問題集「赤本」。最近5カ年収載。
最高の学問を学び、習得する意欲を満たせつつ、日々の勉学に勤しむなら東京大学受験だ。
難関であるが勉学意欲を奮い立たせる。
(レビューより引用)




