算数や数学のセンスは先天的とか後天的とか、おら知らねぇ
よく、「あいつは、もともと頭がいいんだよ！」とか「俺は、もともと頭が悪いから…」といった言葉があちこちで呟かれます。
算数や数学のセンスが先天的か後天的かという論議は、古くから尽きることなく続いているのですが、
- 数学が出来ない人は「先天的だ！」と吐き捨て、
- 数学が出来る人は「後天的だ！」と仰る
これが、たいていの構図だと思いますが、如何でしょうか？
その思い込み様によって、片や興味を惹かれることが手を動かしますから、どんどんセンスが磨かれて来ますし、片や興味を持てないが故に手を動かそうとしませんから、耐えがたい時間を凌ぐだけでセンスなどは生まれようもないということになります。
確かに、体格や性格は当然のこと、運動神経や音感・音楽センスにも先天的な差があるように、数学センスにだって先天的な差があって当たり前のことなんですが、だからといって、学んだり楽しんだりすることを放棄してしまうと、このように大きな差に増幅されてしまうことを、どのように判断されるのかという問題に帰ってきます。
運動神経や音楽センスであれば、自分はダメだけれど、これらに優れている人をは尊敬したりする傾向が強い一方、なぜか、数学センスに優れていたりする人には「何が偉いねん？」と軽蔑する傾向が少し強く出てくるところが不思議です。
まさに、毛利 衛 先生が語られたように「よく勉強だけではなく、他の特技をもった子供達も評価するべきだという論調を耳にするが、事実は全く逆で、スポーツは評価しても、音楽は評価しても、勉強は評価しない。」風潮が、日本では出来上がってしまった現象を垣間見るかのようです。
まぁ、音楽やスポーツは受け身としての楽しみや快感を提供してくれる分野である（主体としての自分と競合することは絶対にない別世界）ことに比して、後者は、主体としての自分が身を置く社会では自分の競合相手になり得るということが、無意識的な嫉妬や劣等感として表出してしまう面もあるのではないかと分析できそうです。
さて、よく、「何故だろう？」という子どもの疑問に上手く答えられないことが子どもの興味を潰すという論が語られます。
もちろん、大局的にはそうなんだろうと思いますが、疑問すら持たなかった子が、何かの拍子に突然興味を抱いたりすることもあります。
どこまでが先天的でどこからが後天的などとの線引きなど出来るものではありません。
ただ、言えることは、前者は「先天的だ！」という言い訳をすることによって、数学のセンスを養うことによるメリットを自ら放棄してしまっているということだけは確かだということですね。
そして、こうなってしまうケースの多くは、算数や数学の世界に留まらず、あらゆることに対して連鎖するものであり、それこそが問題とすべき本質ではないでしょうか？
スポーツができないと「スポーツなんかできたってクソの役にもたたねぇ」、音楽ができないと「音楽なんてクソの役にもたたねぇ」と、あらゆることに対して「できない自分」を正当化しようとするものです。
その言い訳体質こそが「先天的なのでは？」と切り返してはダメですか？
これは冗談ですが、おおかたの本当の舞台裏は、努力してどんなことでもトライすることに意味があることを、環境から教えられなかった、学ばなかったということに尽きるでしょう。
ですから、ここでは、「先天的な要素もあり、後天的な要素もあり！」は明確である以上、どちらが優勢かなどといった不毛の暇人論議は控えて、算数や数学のセンスの扉を開けるためのいくつかのヒントを時とともに重ねていこうと思います。
今は、「何事に対しても一生懸命に分かろうと努力することこそがセンスへの入場券を手に入れることだ」とだけ申し上げておきましょう。
算数・数学センスとは「理解力」と「整理力」「分析力」から生まれ「連想力」「想像力」に帰結するものであり、真剣に刻んだ経験と比較対照しながら知識を整理していく経験の場数を積み重ねることで生まれてくるものです。
音楽のセンスとて同じじゃないですか？
その結果、音楽の音色も数学の数式も美しくなっていくのです。
数学の場合、東にシンプルで美しい出力をする人がいれば、積み重ねをしない人には単に「ズルい」「卑怯なやつ」としか映らないことになってしまうところに哀しさが漂います。
算数・数学センスへの扉 | 前提的2要素
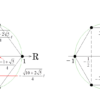
- 169や196という数字を見れば、瞬間的に何かを想起しますか？
（小学生以上：算数センスの第二歩＝数字を分節して見る） - 17×18や19×16という計算を見て、暗算で答が出せますか？
（小学生以上：算数センスの第一歩＝楽をして計算する） - 与えられた式の中に
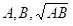という並びを見れば、瞬間的に想起することがありますか？
（高校生以上：算数センスの第二歩とリンクする）
もし、瞬間的に想起するのだとすれば、君は問題の場数をある程度踏んだことで、その結びつきをはっきりと意識する時を刻んだということ。
君が不動産会社に就職すれば、「180㎡でほぼ正方形ですから、縦横の長さは約13ｍと14ｍの真ん中ぐらいですかね！」と即答できることになる。
次の項目のように13×13、14×14は暗算でもできるけれど、これぐらいの数なら計算すらせずに「169、あっ！13×13じゃん」と自然に反応できるまでに対応しておかなくちゃいけません。
暗記じゃないですよ！一つ一つを丁寧に積み重ね、一つ一つから教訓を得る積み重ねをする姿勢で勉強していれば、条件反射で出てくることです。
そうではなく、機械的に暗記して条件反射で出すのであれば、センスのセにも繋がることはないと思いますよ。
前の例の逆算になる13×13、14×14は、九九と同じように条件反射、もしくは、頭の中で暗算ですぐに出せる訓練はしておきたいもの。
本例の前者だと、17が10個の170に、17が8個の136を足して306と答えを出す子が多いのじゃないかと思いますが、結構時間がかかるんじゃない？
それに、なんだか間違える確率も一向に減らない場合は、「間違えるぐらいなら筆算をした方がまし。」の感覚でいた方がいいと思うよ！
もう一つ言っておくと、もっと瞬間的に答えを出す方法があります。
片方の17に他方の一の位8を足して25。（片方の18に他方の一の位7を足しても同じ）
これは百の位と十の位と考えて250。次に、7×8＝56。この2つを足して306が答。
筆算の形をイメージすれば、その理由が分かると思うのですがどうですか？
知ってる子は知ってるだろうけれど、別に知らなくても全然かまわない知識。
知ってるだけで偉そうにしている子は相手にしなくてもいい！
しかし、理由を必ず考えてみることをするならば、センスに繋がっていく大切な作業になってしまうんだね！
10～19の整数同士の掛け算にしか通用しないこと、20以上の整数が混じった場合や20以上の整数同士の場合はどうなるかも併せて教え、そんな場合は「かえってややこしいね！」と流せるように指導してあげれば尚最高です。
おそらく、相加・相乗の不等式は、そのままの形が出てくるから気が付くでしょうが、もう一つの基本的な式とリンクさせて連想してほしいのですね。
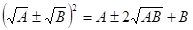という式なんだけれど、√が入ると気が付かないのではないかな？
だとするならば、算数センスの第二歩＝数を分節して見る力の鍛錬経験がないか少ないかのいずれかに起因するものだと分析されます。
「算数・数学センスへの扉」と言い得るのは、たかだかこの2要素だけと私たちは考えています。
多くを挙げ過ぎると、気持ちを分散させてかえって何もしないままに終わってしまうことを知っていることもありますが、正味、「センスの扉」というのは、たかだかこの2つに集約されます。
とはいっても、「算数センスの第二歩＝数字を分節して見る」力は、様々な形で、すべてと言っていいほどに至る問題にて駆使しなければならない共通のリテラシーと言えますので、「扉」としての位置づけとともに「要」として位置づけています。
これを、もう少し拡張した「算数・数学センスへの道」というべきものは、次のコンテンツに譲ることにしますので、下記をご参照ください。
そして、これらを具体的に理解いただくためには、小学生にしろ高校生にしろ、「帝都大学へのビジョン」及びその資料群で感じていただくしか道はないと思います。
最後に申し上げておきますが、当ブログでコンテンツにしている問題や「帝都大学へのビジョン」及びその資料群で使っている問題は、そのほとんどが「数字を分節して見る力」を養うためにあるといっても過言ではありません。
さらに、小学生から高校生まで共通して算数・数学センスを鍛えることのできる最適な素材は、分数・整数、及び、これらで構成される数列であることも申し上げておきましょう。
モンテッソーリ教育と算数・数学
「算数・数学センスへの扉」から、もう少し進んだところにある「算数・数学センスへの道」というべきものは別ページに譲りましたので、ここでは、もっと扉に近いところのお話に切り替えたいと思います。
実は、標題にある「モンテッソーリ教育」に関しては、ブログではあまり書いてません。
それというのも、「帝都大学へのビジョン」の別冊2に当たる「子育て18切符：学習の本質発 モンテッソーリ経由 ロマン行」に、我が子たちを真正のモンテッソーリに通わせた経験をまじえながら記しているからに他なりません。
ネタばれになることは今までの購入者さんのご不快を買うことになりますので、本質は一切語りませんが、結論だけ言いますと、モンテッソーリ教育が算数や数学センスに直結するわけではありません。
とは言っても、悪い方向性で作用することは絶対にあり得ないことだけは確かと判断します。
別に、九九も小学校5年生まで完璧に言えなかった娘が、その後は「東大でも行けるほど考える力が素晴らしい」などと評価されたからではありません。
当たり前のことですが、モンテッソーリ教育の理論及び教具は、算数や数学に秀でるため、あるいは将棋に強くなるためにあるものでも、天才にするためにあるものでもないからです。
一言で言えば、全面的な発達をアシストする中で、自分の得意なことを見つけ、活き活きとした人生をそれぞれの子どもたちが送れるための素地・土台を作るための教育理論であり教育手段です。
もちろん、結果として算数・数学を伸ばす素地を作る可能性はきちんと仕込まれていますよ。
それは、フレーベル教育理論や教育手段である「恩物」にも同じことが言えます。
どうも、そこのところを歪曲して「英才教育」に繋げて商売にしたい輩の方が多いことが、親心を惑わす元凶になっているようですね。
モンテッソーリ教育は経験及び科学的考察によって周到に用意された「教具」に特徴があるわけですが、その中には「数の教具」「感覚の教具」というジャンルの教具があります。
日本の一般的な保育・幼稚園では、算数や数学に繋がっていく数学的知性や空間感覚把握知性、論理的知性を刺激する教育はなおざりにされている傾向が強いですので、その意味では、算数力や数学力に繋がっていく素地ができる可能性は高いと言えるかもしれません。
また、特に空間感覚把握知性においては、フレーベルの「恩物（おんぶつ）」と呼ばれる「教具」に関しても同じことが言えるでしょうか！
確実に断定できない具体的理由の一つは、モンテッソーリでは子どもたちがしたい「〇〇〇」を尊重しますので、「数の教具」「感覚の教具」の教具に一切興味を示さずに経験しない場合があるからです。
あまりの偏りを観察した場合、教員の裁量で「これもしてみない？」と誘うことはあるかもしれませんが、それとて確定的なものではないでしょうからね。
一つだけ進言申し上げておきたいことは、「モンテッソーリ教育」には認定制度はありませんが、モンテッソーリ協会の資格認定を受けた教員が居ないようでは正式な「モンテッソーリ教育」の園とは呼べません。
併せて「英才教育」だの「天才を育てる」などというキャッチフレーズが掲げられているのであれば、それはモンテッソーリの名前を利用しているだけであることは明々白々でしょうね。
モンテッソーリ教育の正式な教育を受けてすら、M.モンテッソーリ女史は、指導者の質を心配されていたほどだということを、頭に入れておかれることは、保護者のあなたにも有益なことだと思います。
モンテッソーリの教具だけを調達・準備して、その一つ一つの教具の意義すら理解していない指導者のもとで「モンテッソーリ教育採用！」だけが謳われることが多いでしょうから、しっかりと見極める力が必要です。
最後に一つ加えておくとすれば、モンテッソーリ教育の日本における第一人者の方の著作にて、「知恵・知性の4大要素」を見ますと、私たちが本編や算数・数学の資料で、具体的な指導指針として使う言葉と見事にオーバーラップしています。
それ以上に、モンテッソーリ女史が最重要とみなした「〇〇」という概念は、私たちが「やる気」という面で最重要視する「日常生活における△△」という概念と1：1に対応するとみなしています。
これらの理論を綜合しますと、各教科を個別に伸ばすことを考えるより、「知恵・知性」全体を育むという共通した考えを持つことの妥当性と賢明さが浮かび上がって来ます。
家庭でモンテッソーリを採り入れたいと思われるなら、モンテッソーリ教育に関する論文や書籍は結構出ていますから、商売人の浅薄な言葉だけに洗脳されるのではなく、広く深く研究されれば上手く活用できるのではないでしょうか？
必ず、然るべき人の然るべき論文に目を通されんことをおすすめ致します。
併せて、本編でも根拠として言及しています神経科学（脳科学）と対照されますと、モンテッソーリやフレーベルの科学的実証主義の先見性が理解できるのではないでしょうか。
これらの本質を学ばれ、デメリットが心配される事柄に関しては対処策をも想定しておかれるのであれば、家庭での教育にも採用できることは多くあると考えます。
さすれば、
などの教具を家庭で導入されるのも、たとえ良き指導に巡り合うことがなくとも、自前で有効な働きかけの一つができるのではないかとも考えます。
その「一つ」の積み重ねが、よりベターな子育てとなっていくことでしょう。
算数・数学センスの要を鍛える
算数のセンスを身に着けるためのスタートラインは、最も上流にある源泉中の源泉「数に対するセンス」を鍛えることに尽きます。
一言で言えば、「数を多点カメラで見る＝分節して考える力」です。
すべての単元に絡んできますから、綜合的な算数力・数学力を決める要になります。
たとえ、難関の進学校に入学できても、中高と進むにつれて数学ができなくなっていく場合は、ここが鍛えられていないことが表面化してくるということに過ぎません。
ですから、大学受験で数学がネックになっている場合も、極端に言えば「先に、難関中学の算数入試過去問題を自力で解き切るぐらいのレベルにする方が早道だよ」とすら言っても過言ではないと思いますよ。
その具体的な内容は、高校数学であろうが小学算数であろうが、脳細胞の動きを視座として資料の中に多く散りばめています。
中学受験を目指すお子さんの保護者さんにも、算数・数学のセンスを養う源泉を突く資料として、下記を資料としておりますのでご参考にされてください。
ある意味、この17問だけでも、丁寧に理解するように噛みしめれば、算数・数学のセンスは一挙に飛躍する可能性が高まることでしょう。
まぁ、いつの時代も変わりなく存在する真面目に勉強する層を除いては、
- あまりにも、日本語の語彙レベル、及び言葉を扱う力が欠如している。（とうてい読解力などのレベルではない：大きくはスマホ、その中でも特にSNSの影響でしょうが…）
- 感情を表現する言葉だけには長けているが、論理的な接続など全く意識すらない。（SMNSはじめ、単語の羅列文化の影響）
- したがって、数学語に変換することなど到底できませんし、真っ当な世界であれば必須とされる論理性すらないことにどうも思わない。
- ですから、逆に数学語を日本語で理解する気もないし、しようともしない
これが、ゆとり教育で落ちたところに、安易なSNS社会がさらに追い打ちをかける社会の現実となっています。
2009年にZ会の担当者様よりいただいたメールでは、かなりできる層ですら明らかに数学力は落ちているようですから、スマホ三昧の今ではどうなのかを想像すると恐ろしい気もします。
ただ、どの国でも同じ傾向ですから、少しは安心できるものの、韓国と肩を並べて世界有数のエンタメ好き・情報弱者であることは間違いない種族のようですから、相当世界の中では厳しいポジションに堕ちていくことは容易に想像されます。
ぶっちゃけた話、2012年以降は、マジョリティと呼ばれる世界ではこういった状況ですが、悲しむべきでないのは、そうならない層はいつでも健在に存在するということです。
「帝都大学へのビジョン」に付属した中学受験生向け資料の詳しくは、
