3つの整数で遊んで算数のセンスを揺さぶっておこう!
次の問題を考えてください。
中高生の諸君も小学生の問題だからといって無視せずにトライしてみてください。
中学生・高校生になって数学がだんだんと分からなくなるのも、こういった整数に親しんでいないところに、大いにその元凶があるものです。
小学生のお子さんをお持ちの保護者さんならば、「一緒に考えてみない?」って持ち掛けてみてください。
決して、子どもさんに勝とうとしたり「なんで分からないのよ」なんて言ってはダメですよ!
発想を導いたり発想を出し合う姿勢で進めてくださいね!
誰もが知るところの整数に関する問題は、自分で考え切れるようになるまで訓練するところに意味があります。
見るだけで嫌気がさす数学数学した問題ではなく、考える作業を始める敷居が低い問題を利用してやり切ることを覚えると、勉強全体において勉強を始めようとする習慣を後押ししてくれます。
その時に分からなくても、明日気分を入れ替えてトライすることも出来ますから、出来る限り答えをすぐに見ないで考え切ってください。
そこまで頑張ってこそ、どうしても分からないときに答えを見て自分の思い至らなかったところを自覚することがものすごく有効になります。
【問題】分からない3つの整数を特定する
【問題】
3つの数A,B,Cがあり、AとB、BとC、CとAの積がそれぞれ、432,792,264のとき、3つの数はそれぞれいくらでしょう。
問題を見ただけでやり方を知っている子は、すぐに式で解き始めると思います。
式を書いているということは、意味も分かっていると思いますが、出来れば、何故そのように解くのかを友達に日本語で説明できるようにはしておいてくださいね。
図やマンガで表してみよう!「輪環の順」も知っておこう!
さて、こんな問題初めてだって子は、素直に下のような図にまとめてみることを経験してみてください。
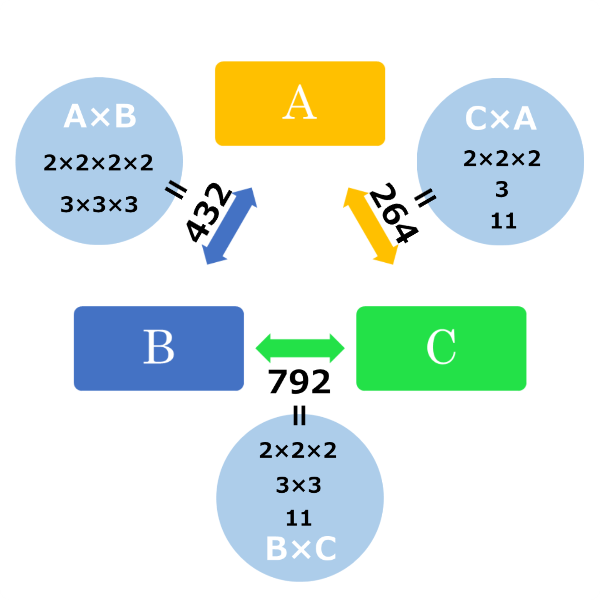
このように、A,B,Cという3つの文字で問題が組まれている場合は、縦一列に並べて書くよりも、上図のように3角形の頂点や円形3等分位置に配置して書くと分かりやすいことも頭に入れておかれるといいですよ。
A×B、B×Cの後は、A×CではなくC×Aと書くように決めておかれると(「輪環の順」と呼び、3文字の場合だけに有効)、絶対そう書かないといけないというわけではありませんが、どの数に対しても平等な書き方をしておく方が美しく、しかも理路整然として整理もしやすく間違いが少なくなりますから、中高生になっても役に立つと思いますよ。
この問題は、
【3つの数A,B,Cがあり、AとB、BとC、CとAの和がそれぞれ、〇,△,□のとき、3つの数はそれぞれいくらでしょう。】って問題にもできますよ。
そんなとき、A+B、B+Cの後は、A+CではなくC+Aと書くように決めておかれるといいですよってことが「輪環の順」ということなんです。
ところで、この図を見て、何かヒントは得られましたか?
よーく観察してくださいね。
私は、「それぞれは一つの文字が欠けているけれど、全体として眺めたら平等に登場してる」ってことに気付きました。
なら、AとBの積、BとCの積、CとAの積を全部掛けちゃったら、平等になるんじゃねぇ?
(A×B)×(B×C)×(C×A)となって、どの文字もみんな平等に2個ずつ登場しちゃう!!
ということは、(A×B×C)×(A×B×C)=432×792×264 ってことじゃん!
(A×B×C)の答えになる数同士を掛ければ右の計算した答えになればいいってこと。
でも、こんな計算はしたくもないし、計算したって同じ数を掛けてこんな大きな数になるような数を探すのは面倒くさいなぁ。(小学生なら「できないよぅ!」になりますね。)
素因数分解登場!
そんなこともあろうかと、上の図では、それぞれの積をバラバラに分解しておいたんですよ。
『素因数分解』って奴ですね。
こうしておけば、(A×B)×(B×C)×(C×A)の結果、即ち(A×B×C)×(A×B×C)の結果は2の掛け算が何個、3の掛け算が何個、11の掛け算が何個って表現で表せます。
そうすると、同じ数を掛けた結果、2の掛け算が〇個、3の掛け算が△個、11の掛け算が□個ってことになりますから、これを平等に分け合えば、それが元の数ってことになりますよね。
整数を見たら、掛け算の形に変身させておくと何かと便利そうだということが分かりますね。
本内容は「素因数分解と輪環の順」にて脳細胞の働かせ方として詳しく資料化しております。








