[脳細胞を働かせてちょう題 07]ハノイの塔の問題
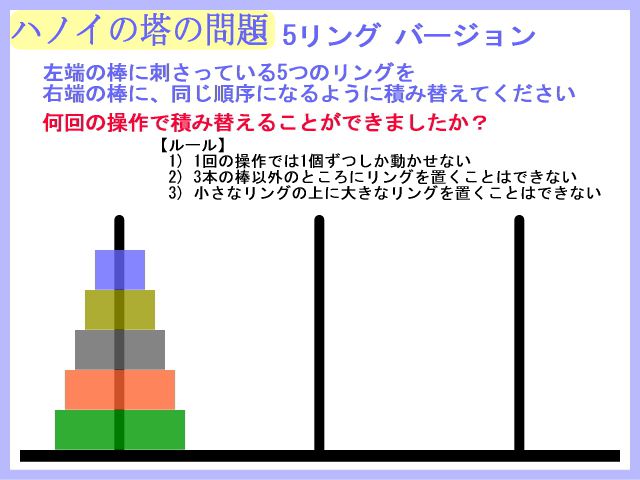
上の問題を解いてみてください。
知育玩具としても商品として販売されている有名な【ハノイの塔】と呼ばれる問題です。
別名【ブラフマーの塔】
数年前、テレビドラマの『探偵ガリレオ』で【フィボナッチ数列】とともに一躍有名になった【リュカ数列】の産みの親【エドゥアール・リュカ】が考案・販売したとされています。
大学入試でも、名前を出されることもなく、それとなく出題されるこれらの数列は、資料「数学への導火線3:フィボナる・リュカる(PDF40ページ)」で漸化式の正体を兼ねて執筆していますので、購入者さんは、この資料で「漸化式」の問題が出てほしくてたまらないほどになるでしょう。
近年は、旧帝大や一橋で、確率の漸化式の問題がよく出ているようですね。
東大の過去問は資料の過去問着眼点でも詳しく説明していますから、よくなぞっておかれると大いに得するかもしれませんよ。
冒頭でも記しましたが、本ページは当サイトの中でも、とても人気のあるページです。
ですから、追記しておこうと考えたのですが、この問題だけでいいですから、また、何日かけてもいいですから、自分で納得いくまで、そのルールをとことん暴き出そうとしてください。
それを試みることだけでも、あなたは「脳を働かせる感覚」を体で覚えることになると思います。
パターンを覚えるために10題やる暇があるのでしたら、5題に抑えて、この問題一つを大切に突き詰めてみて下さい。
さすれば、いつでも本質を見つけて解答できる力をつけていくことができます。
ところが、何ごとでも中途半端に「何となく」で済ませてしまうことは、すべてのことに通じてしまうものですから、考える力が生まれる瞬間も場合も失くしてしまいます。
ぶっちゃけた話、下のように道理や理屈を悩みながらでも、レポートにしてやろうというぐらいの気楽な気持ちでやり切れば、もうそこで、あなたが賢いと思っている人と同じレベルになっていると思いますよ。
普通に賢い人との差なんて、実はこういった些細なところで決まってしまっているのです。
入試で必ず1問では問われる「洩れなく整理する能力」
僕も、「勉強へのきっかけ作りとして【ハノイの塔】もいいですね!」と書いたままでそのままにしていましたので、このあたりで少し追求してみようかと思います。
中学入試にしろ大学入試にしろ、算数・数学の問題で必ず出題者が見たい能力の一つが、整理して洩れなく可能性を書き出せるかどうかの能力です。
この力を見る問題は必ず1問は入っていると言っても過言ではありませんが、その能力をゲーム感覚で育む素材として「ハノイの塔の問題」は適していますので、知育玩具になっていることも頷けます。
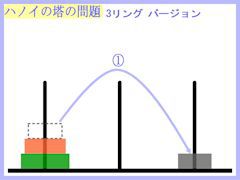
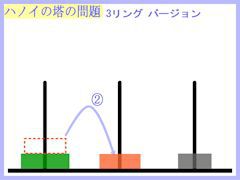
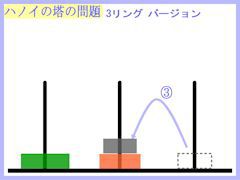
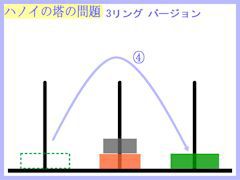
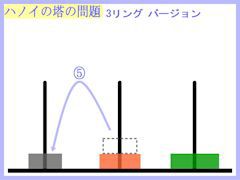
さて、この問題の内容は画像に示した通りです。
積み替えるリングの数によって難易度が変わってきそうなことは容易に想像できますよね。
最初にトライするには、5個バージョンが最も手頃ではないでしょうか?
残念ながら、僕はゲームソフトを作る知識は全くありませんのでビジュアルなゲームとしては、この場でご提供できませんが、下記のサイトで、クリック&ドロップで簡単に楽しめます。
何手で(何回の操作で)完成したかのカウントも出てきます。
僕なんか始めてトライしたときは、恥ずかしながら44~5手かかっていたように記憶しています。
最初は何も考えずに感覚でやるもんで致し方ありませんが、久しぶりにやってみたら34手。
・・・情けないことです!感覚でやっても、結果、それが=論理的に直結していないと、一流とは言えません。
私たちが自身を二流だと自己判定して、あちこちで述べている所以はそこにあります。
最小で済ませる手数は後のお楽しみに取っておいて、あまり難しく考えずにどんどん手を動かして試行錯誤しながら挑戦してみてください。
気が付けばできてるって感じで完成すると思いますよ。
↓現在、ページはリニューアルされて、スクリプトも正常に機能しています↓
まずは3個のリング(レベル1)から始めてみては如何でしょうか?
理屈を考えながら1回トライするごとにリセットして何回かトライし、10秒前後で完成させることが再現出来れば、リング数を増やしても理詰めで攻めていける第一歩になると思いますよ。
4個のリングはレベル2で楽しめます。
3個のリング(レベル1)で、ある程度コツは掴めたかもしれませんね。
この時に、完成までの時間ではなく、完成までの回数に注目するようにしてください。
何回かトライして、手数(操作回数)が減ってくれば、コツを修得しようと脳を働かせているって証拠になりますね。
クリアーできれば、5個のリング(レベル4)、6個のリング(レベル5)、7個のリング(レベル7)でも楽しんでみて下さいね。
- レベル3は2列の5個リングを他の2列に移し替える5本棒タイプ
- レベル6は2列の5個リングを他の2列に移し替える4本棒タイプ
その前に、5個リングへのトライが一段落したところで「どういう規則で動かしていけばいいんだろう」ってことを整理しておくと、リングの数が多くなったときに、サラサラと最短の手数で完成させるようになれるでしょう。
それに、頭の体操としても、やりっ放しじゃなくて、きちんと理屈を整理しておくことが大切ですからね。
さて、何手動かせば課題を遂行できるか?
興味が湧いてきましたか?
今や、ネットでも【ハノイの塔の問題】は詳しく解説したサイトも多いのに驚きました。
でも、最小の手数は”2n-1(nはリングの数)”とどれもが書いていますが、何故”2n“が出てくるのか、よく説明されていないコンテンツも多いように見受けられました。
木のおもちゃ製作所・銀河工房
ブラフマーの塔
インドのガンジス河の畔のベナレス(ヴァラナシ)に世界の中心を表すという聖堂がある。
そこには3本の大理石の柱(ダイヤモンドの針との説もあり)が立てられており、そのうちの1本には、当初64枚の黄金の円盤が大きい円盤から順に重ねられていたという。
バラモン僧たちはそこで、一日中円盤を別の柱に移し替える作業を行っている。
そして、全ての円盤の移し替えが終わったときに、この世は崩壊し終焉を迎えると言われている。
もちろんこれはリュカの作り話であるが、64枚の円盤を移動させるには、最低でも18,446,744,073,709,551,615回かかり、1枚移動させるのに1秒かかったとして、約5,845億年かかる(なお、ビッグバンは今から約137億年前の発生とされている)。
小さい数でバカみたいに幼稚にプロセスを追う!
さて、数の問題を考えるには、「やっぱり数が小さいものから考えることで、何かが見えてくるよ」ということは、本編でも【過去入試問題の着眼点】などでも口をすっぱくして言ってましたね。
では、その通り、リング数が少ない場合に置き換えてみて、バカみたいに幼稚にプロセスを追ってみましょう。
何もカッコ悪いことではありません。
とは言っても、リング数が1個の場合は、ただ左端から右端に移すだけの1手で済みますから、割愛しますね。
まさか、一旦中央の棒に刺して、次に左端の棒に刺すという2手で完成させる子も居ないでしょう。
それもアリですが、どう褒めてあげようか悩みどころです…。(笑)
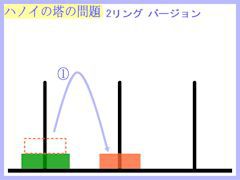
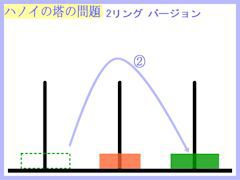
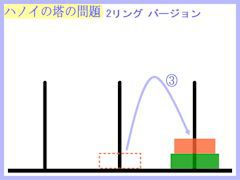
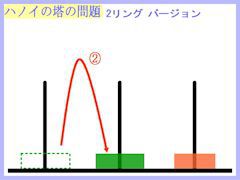
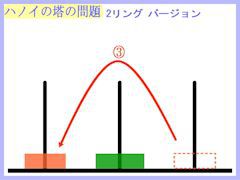
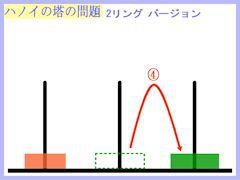
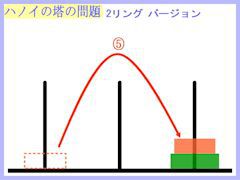
では、リング2個バージョンの操作を下に表してみますね。
↑クリックで画像拡大(以下の小画像は全てクリックで拡大できます。)↑
リング2個なら、全然問題なくできたのではないでしょうか?
たった3手で目的は達成されます。
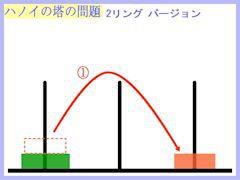
でもね、ここで、最初のリングを一番右端の棒に刺してしまったらどうでしょう?
そのことも可能性としてあるわけですから、この可能性にもきちんと落とし前をつけておかねばなりません。
可能性のあることを放置しておいては、「論理的に考えた」などという資格はとてもあるとは言えません。
この場合は、下のようになり、5手を要してしまいます。
よく眺めてみると、もし右端の棒にではなく中央の棒に積み替えることが目的だったとすれば、第3手目で右端のリングを中央に移せば、それで終了ということになりますね。
もし右端の棒にではなく中央の棒に積み替えることが目的だったとすれば、3手で済んだというわけです。
何かルールがあるのではないだろうか?
どうやら、どの棒にそのままの順序で積み替えるかによって、各操作でリングをどの棒に刺せば無駄が生じないのかを決める規則がありそうですよね!
そんな風な予感がしませんか?
2リングの場合で右端の棒が目的地の場合は、最初のリング(小さい方)は目的地の棒とは違う棒(中央)に刺し、次のリング(大きい方)は目的地の棒(右端)に刺せば、無駄なく最小の手数で目的を達成できますね。
もし3リングであれば、これとは逆のことが言えそうです。
リングが奇数か偶数かで論理が逆転するのではないかと予想されるのではないですか?
この段階で、僕はこの程度の推論を何となく持ちました。
よし、もう1個リングを増やしてみれば、何か掴めるかもしれない!
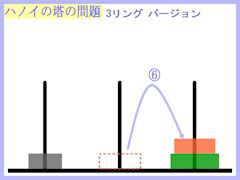
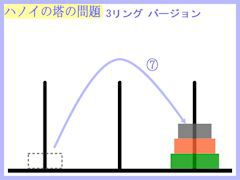
それでは、リング3個バージョンの操作も紐解いておきましょう。
もっと鮮やかに見えてくるのではないかと期待しつつ・・・。
結果、下のような操作の流れとなりました。
少し複雑になりましたが、7手で目的は達成されるようです。
無駄な手数に関しては、やはり予想通り、今回は2リングの際とは逆に、最初に移動させるリングを目的の棒に次に移動させるリングを目的とは別の棒に移すことで無駄が発生しないことが分かりますね。
この辺りからは読んでいるだけでは、分かったようで分かっていない領域に入ってきますから、必ず自分の手で検証し確認しながら進めないと、真にこの問題の本質は分かって来ないと思いますよ。
ここで、ついでに、4リングの場合に思いを馳せてみると、最大のリングの上に載っている3リングに関して、この流れと同じ操作をしたとすれば、真ん中の棒に入れねばなりませんね。
そうなると、再び右端に移すための手数を打たなければなりません。
それならば、同じ手数でできるのですから、最初から上3リングを真ん中の棒に積み替えておけば、最大リングはダイレクトに右端の棒に刺せてしまい、無駄が生じないと考えられます。
ハッハーン!
どうやら、
- 奇数のリング数のときは、最初は目的地の棒に移し変えるスタート
- 偶数のリング数のときは、最初は目的地とは別の棒に移し変えるスタート
を切れば無駄が生じないのだなという一般化に辿り着きます。
さて、7手という数字で、ピーンと来ました~!
2リングは3手、3リングは7手が最小の手数。
そう来れば、ここで想起されるのは、”2n”
これは、ある程度数学のトレーニングを積んできた子であれば、比較的自然に出てくる予測ですね。
でも確証があるわけではありませんから、今はただ頭の隅に置いておくだけでスルーしておき、次に、操作の流れから何か言えることはないかを探してみましょう。
- 僕が注目したのは、第3ステップを終えた段階です。
最初に左端の底にあった最も大きなリングが右端の棒に刺せる準備ができています。
絶対にこの状態を経ることなしに目的は達成できないということが言えますね。 - そして、第3ステップまでの操作の流れはどうでしょう?
よく見ると、左端にあった上2つのリングを隣の棒に積み替える作業ではありませんか!
ちょうど3手で積み替えることができていますね。 - 最後に、第4ステップで最も大きなリングを右端の棒に刺した後はどうでしょうか?
次の課題は、中央の棒にある2つのリングを右端の棒に積み替える作業ではありませんか!
そうなると、ここもちょうど3手で積み替えることができるということになりますね。
何となくゴールが見えて来たら逆手流でゴールから眺めてみる!
7手=3手+1手+3手と分解して考えることで、操作の流れの有り様、意味合いが少し浮かび上がってきましたね。
即ち、【2リングを積み替える手数+最大リングを目的地に移す1手+2リングを積み替える手数】なる構図が見えて来ました。