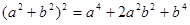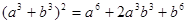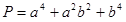 において、
において、
 を因数分解せよ。
を因数分解せよ。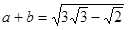 ,
,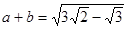 のとき、
のとき、 の値を求めよ。
の値を求めよ。
数学のセンスを引き出すのは難問でもややこしい問題でもなく、基本としっかりキャッチボールできるような本問のような問題です。
出来る子も存外ここが理解できたということで一挙に突き進んでいけるのはこういった基本レベルでありながら体系的に理解を促す良問です。
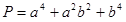 の式の形は非常によく見かける形ですね。
の式の形は非常によく見かける形ですね。
見たことがないという諸君は、多分全然勉強していないか、出会っていても一つ一つの経験を丁寧に取り扱おうという気持ちがなく盲滅法に消化していただけなのだと思います。
そこそこ数学で点を取れる諸君は、問題見ただけで方針が立っているでしょうけれど、「自分の頭の動きを抽象化するとこういうことなんだなぁ!」とか「いや俺のとは違うなぁ!」とか批評しながら客観的に眺めてみるのもいい勉強になるでしょう。
『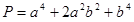 だったらよかったのに!』って思いませんでしたか?
だったらよかったのに!』って思いませんでしたか?
もし思わなかったというのであれば、基本中の基本公式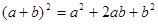 をこれだけではなく次のように並べてみてください。
をこれだけではなく次のように並べてみてください。
ここでは厳密に数学用語では説明しませんが、右辺のダラダラした(この程度じゃ別にダラダラとは言えませんが)式は左辺の簡潔で綺麗な式にまとめることができる(因数分解ができる)ということとして、感覚的に今刻み込んで下さい。
一番上の式しか公式には載っていないから、問題に当たったことがなければ2番目や3番目の等式などを利用するとなると「ずるいヤ!」と思うかもしれませんが、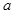 と
と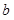 には何が入ろうと構わないのですから、今、この感覚を丁寧に経験しておいてください。
には何が入ろうと構わないのですから、今、この感覚を丁寧に経験しておいてください。
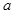 と
と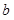 の替わりに
の替わりに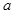 と
と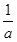 を入れてやると、また違った式が出来上がります
を入れてやると、また違った式が出来上がります
ついでに、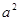 と
と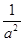 も入れてみてください。
も入れてみてください。
この時に出来る右辺の形も式の変形としての象徴的な式になりますから、これもセットで感覚的に刻み込む作業をすれば、数学センスが突如花開くきっかけになるかもしれません。
ここの感覚を掴んでおくと、本問題の式を見た途端に、頭に刻み込んだ右辺の式が想起されることでしょう。
『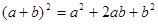 だったら利用できる式があるのに・・・』となります。
だったら利用できる式があるのに・・・』となります。
ここからは、ちょっと違うから「残念」と諦めるのではなく、「こうだったらいいのにな」の形を採用してみて、ちょっと違う分(ここでは差分)は、その後で辻褄の合うように付け足してやるってことを体で覚えてください。
そうすると、この問題の場合は、もう一つの代表的な公式によって見事に解決に向かうことが分かります。
※ALLコース購入者の方で添削希望の方は画像かPDFファイルでお送りいただければ添削させていただきます。
前の「受験数学 勉強の仕方例」は、関数の正体を見破る
次の「受験数学 勉強の仕方例」は、積分した式を微分する着眼点